
分析 构造辅助函数F(x)=f(x)-2x,求导,f′(x)<2,F(x)单调递减,将f(x3)>2x3+2转化成f(x3)-2x3>f(1)-2×1,根据函数单调性得x2<1,即可解得x的取值范围.
解答 解:令F(x)=f(x)-2x,又f'(x)<2,
则F'(x)=f'(x)-2<0
∴F(x)在R上单调递减
∵f(1)=4,
∴f(x3)>2x3+2可转化成f(x3)-2x3>f(1)-2×1,
即F(x2)>F(1),
根据F(x)在R上单调递减则:x2<1,
解得:-1<x<1,
故答案为:(-1,1).
点评 本题利用导数研究函数单调性,根据已知函数构造辅助函数,考查学生会利用函数的单调性解决实际问题的能力,属于中档题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1972 | B. | 448 | C. | 896 | D. | 224 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
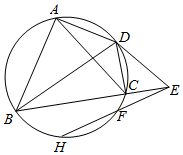 已知△ABC的外接圆为⊙O,∠B的平分线交圆O于D,过D作圆O的切线DE与BC的延长线交于E,连接AD,CD,过E再作圆的割线交圆O于F,H.
已知△ABC的外接圆为⊙O,∠B的平分线交圆O于D,过D作圆O的切线DE与BC的延长线交于E,连接AD,CD,过E再作圆的割线交圆O于F,H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2017}$,$\frac{1}{2015}$) | B. | ($\frac{1}{2016}$,$\frac{1}{2014}$) | ||
| C. | (-$\frac{1}{2015}$,-$\frac{1}{2017}$)∪($\frac{1}{2017}$,$\frac{1}{2015}$) | D. | (-$\frac{1}{2014}$,$\frac{1}{2016}$)∪($\frac{1}{2016}$,$\frac{1}{2014}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
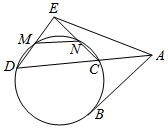 如图,已知AB,ACD分别为圆的一条切线和一条割线,M,N为圆上两点,DM延长线与CN延长线交于点E.
如图,已知AB,ACD分别为圆的一条切线和一条割线,M,N为圆上两点,DM延长线与CN延长线交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com