
| A. | 1972 | B. | 448 | C. | 896 | D. | 224 |
分析 二项式($\frac{x}{2}$+$\frac{2}{\root{3}{x}}$)n(其中n∈N*)的展开式中,第5项的二项式系数最大,可得n=8.再利用展开式的通项公式即可得出.
解答 解:∵二项式($\frac{x}{2}$+$\frac{2}{\root{3}{x}}$)n(其中n∈N*)的展开式中,第5项的二项式系数最大,∴n=8.
∴$(\frac{x}{2}+\frac{2}{\root{3}{x}})^{8}$的展开式中的通项公式为:Tr+1=${∁}_{8}^{r}(\frac{x}{2})^{8-r}(\frac{2}{\root{3}{x}})^{r}$=22r-8${∁}_{8}^{r}$${x}^{8-\frac{4r}{3}}$.
令8-$\frac{4r}{3}$=0,解得r=6.
∴展开式中的常数项=${2}^{4}{∁}_{8}^{6}$=448.
故选:B.
点评 本题考查了二项式定理的通项公式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
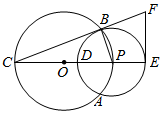 如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB的延长线于点F.
如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-$\sqrt{x}$ | B. | y=$\frac{1}{x}$ | C. | y=ex-e-x | D. | y=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{5}$ | B. | $\frac{2π}{5}$ | C. | $\frac{3π}{10}$ | D. | $\frac{9π}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com