
分析 (1)设所求直线的方程为y=$\frac{3}{4}$x+b,由此求出纵截距y=b,横截距x=-$\frac{4}{3}$b,由已知得 $\frac{1}{2}$|b•(-$\frac{4}{3}$b)|=6,由此能求出直线方程.
(2)根据两条直线平行的条件,建立关于m的关系式,即可得到使l1∥l2的实数m的值.
解答 解:(1)设所求直线的方程为y=$\frac{3}{4}$x+b,
令x=0,得y=b,
令y=0,得x=-$\frac{4}{3}$b,
由已知,得$\frac{1}{2}$|b•(-$\frac{4}{3}$b)|=6,
即$\frac{2}{3}$b2=6,解得b=±3.
故所求的直线方程是y=$\frac{3}{4}$x±3,即3x-4y±12=0.
(2)解:当直线l1∥l2时,$\frac{m}{1}$=$\frac{1}{m}$≠$\frac{-m-1}{-2m}$
解之得m=-1(m=1时两直线重合,不合题意,舍去),
直线l1:x-y=0和直线l2:x-y+2=0,
两条平行线之间的距离为:d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
点评 本题考查直线方程的求法,两条直线平行的情况下求参数m的值.着重考查了直线的方程与直线的位置关系等知识,属于基础题.在判断两条直线平行时,应该注意两条直线不能重合,否则会出现多解而致错.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{5}$ | B. | $\frac{2π}{5}$ | C. | $\frac{3π}{10}$ | D. | $\frac{9π}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
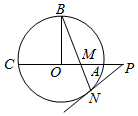 如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线CA的延长线于P.
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线CA的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2017) | B. | (0,2018) | C. | (2017,+∞) | D. | (2018,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
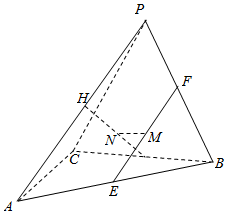 如图,在四面体PABC中,平面PBC⊥平面ABC,△ABC为等腰直角三角形,且∠C=90°,PB=PC,点E,F,G,H分别是线段AB,BP,BC,PA的中点,点M,N分别是EF,GH的中点.
如图,在四面体PABC中,平面PBC⊥平面ABC,△ABC为等腰直角三角形,且∠C=90°,PB=PC,点E,F,G,H分别是线段AB,BP,BC,PA的中点,点M,N分别是EF,GH的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com