
分析 (1)由椭圆的方程可知焦点在x轴上,c=1,由a2=b2+c2,求得椭圆方程为$\frac{{x}^{2}}{{b}^{2}+1}+\frac{{y}^{2}}{{b}^{2}}=1$,将点M(1,$\frac{3}{2}$),代入椭圆方程,即可求得a和b的值,写出椭圆方程;
(2)直线l的斜率不存在时,P,Q两点关于x轴对称,x1=x2,y1=-y2,由三角形面积公式即可求得|x1|和|y1|的值,可知x12+x22和y12+y22均为定值,当直线斜率存在,设出直线方程代入椭圆方程,利用△>0及韦达定理求得x1+x2和x1•x2的关系,利用点到直线的距离公式和弦长公式求得△OPQ的面积,求得a和k的关系式,即可证明x12+x22为定值,利用y1=kx1+b,y2=kx2+b,即可求得y12+y22为定值;
(3)根据中点坐标公式,求得4丨OM丨2+丨PQ丨2的值,根据基本不等式,得丨OM丨•丨PQ丨≤$\frac{7}{2}$,即可求得|OM|•|PQ|的最大值.
解答 解:由题意得:焦点在x轴上,c=1,a2=b2+c2,即a2=b2+1,
椭圆方程变为:$\frac{{x}^{2}}{{b}^{2}+1}+\frac{{y}^{2}}{{b}^{2}}=1$,将M(1,$\frac{3}{2}$),代入椭圆方程,
整理得:$\frac{1}{{b}^{2}+1}+\frac{9}{4{b}^{2}}=1$,解得b2=3,a2=4
∴椭圆方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)当直线l的斜率不存在时,P,Q两点关于x轴对称,
所以x1=x2,y1=-y2,
∵P(x1,y1)在椭圆上,
∴$\frac{{x}_{1}^{2}}{4}$+$\frac{{y}_{1}^{2}}{3}$=1,
△OPQ的面积为$\sqrt{3}$,|x1||y1|=$\sqrt{3}$,
∴|x1|=$\sqrt{2}$,|y1|=$\frac{\sqrt{6}}{2}$,
x12+x22=4,y12+y22=3均为定值;
当直线l的斜率存在时,设直线l的方程为y=kx+b,
将其代入椭圆方程整理得:(3+4k2)x2+8kbx+4b2-12=0,
△=(8kb)2-4(3+4k2)•(4b2-12)=48(3+4k2-b2)>0,即3+4k2>b2,
由韦达定理可知x1+x2=-$\frac{8kb}{3+4{k}^{2}}$,x1•x2=$\frac{4{b}^{2}-12}{3+4{k}^{2}}$,
∴丨PQ丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=4$\sqrt{3}$•$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{3+4{k}^{2}-{b}^{2}}}{3+4{k}^{2}}$,
点O到直线l的距离为d=$\frac{丨b丨}{\sqrt{1+{k}^{2}}}$,
则△OPQ的面积S=$\frac{1}{2}$•d•丨PQ丨=$\frac{1}{2}$•$\frac{丨b丨}{\sqrt{1+{k}^{2}}}$•4$\sqrt{3}$•$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{3+4{k}^{2}-{b}^{2}}}{3+4{k}^{2}}$=2$\sqrt{3}$•$\frac{\sqrt{3+4{k}^{2}-{b}^{2}}}{3+4{k}^{2}}$,
即2$\sqrt{3}$•$\frac{\sqrt{3+4{k}^{2}-{b}^{2}}}{3+4{k}^{2}}$=$\sqrt{3}$,整理得:3+4k2=b2,满足△>0,
∴x12+x22=(x1+x2)2-2x1•x2=(-$\frac{8kb}{3+4{k}^{2}}$)2-2$\frac{4{b}^{2}-12}{3+4{k}^{2}}$=4,
y1=kx1+b,y2=kx2+b,
∴y12+y22=k2(x12+x22)+2kb(x1+x2)+2b2=4k2-8k2+2b2=3,
综上可知:x12+x22=4,y12+y22=3均为定值;
(3)4丨OM丨2+丨PQ丨2=(x1+x2)2+(y1+y2)2+(x1-x2)2+(y1-y2)2,
=2[(x12+x22)+(y12+y22)]=14,
所以2丨OM丨•丨PQ丨≤$\frac{4丨OM{丨}^{2}+丨PQ{丨}^{2}}{2}$=7,
即丨OM丨•丨PQ丨≤$\frac{7}{2}$,当且仅当21OM丨=丨PQ丨=$\sqrt{7}$时等号成立,
因此丨OM丨•丨PQ丨的最小值为$\frac{7}{2}$.
点评 本题考查求椭圆的标准方程,直线与椭圆的位置关系,弦长公式和点到直线的距离公式,是一道综合性的试题,考查了学生综合运用知识解决问题的能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
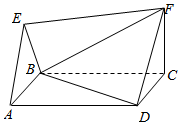 如图,等腰直角三角形ABE与正方形ABCD所在的平面互相垂直,AE⊥BE,AB=2,FC⊥平面ABCD,且FC=1.
如图,等腰直角三角形ABE与正方形ABCD所在的平面互相垂直,AE⊥BE,AB=2,FC⊥平面ABCD,且FC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4029 | B. | 4031 | C. | 4033 | D. | 4035 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com