练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x＜0}\\{lnx，x＞0}\end{array}\right.$，则f[f（$\frac{1}{e}$）]=（　　）
    A．-$\frac{1}{e}$B．-eC．eD．$\frac{1}{e}$

    分析 由已知条件，直接利用分段函数的定义先求出f（$\frac{1}{e}$）=ln$\frac{1}{e}$=-1，由此能求出f[f（$\frac{1}{e}$）]．

    解答 解：∵f（x）=$\left\{\begin{array}{l}{{e}^{x}，x＜0}\\{lnx，x＞0}\end{array}\right.$，
    ∴f（$\frac{1}{e}$）=ln$\frac{1}{e}$=-1，
    f[f（$\frac{1}{e}$）]=f（-1）=e-1=$\frac{1}{e}$．
    故选：D．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．三角形的两边分别为3cm，5cm，它们所夹角的余弦值为方程5x2-7x-6=0的根，则这个三角形的面积为（　　）
    A．6cm2B．7cm2C．9cm2D．10cm2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．函数r=f（P）的图象如图所示
    （Ⅰ）函数r=f（P）的定义域和值域分别是什么？
    （Ⅱ）r取何值时，只有唯一的P值与之对应？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．一个完整的程序框图至少包含（　　）
    A．终端框和输入、输出框B．终端框和处理框
    C．终端框和判断框D．终端框、处理框和输入、输出框

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知$A=\{x|\frac{2x+2}{x-2}＜1\}$，B={x|x2＞5-4x}，C={x|m-1＜x＜m+1，m∈R}
    （1）求A∩B；
    （2）若（A∩B）⊆C，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=$\left\{{\begin{array}{l}{x（x+4），x≥0}\\{x（x-4），x＜0}\end{array}}$，若f（a）＞f（8-a），则a的取值范围是（　　）
    A．（-∞，4）B．（-4，0）C．（0，4）D．（4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

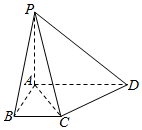    17．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，∠ABC=90°，AB=BC=2，PA=AD=4．
    （1）求证：CD⊥平面PAC；（2）求二面角C-PD-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．先后任意地抛一枚质地均匀的正方体骰子两次，所得点分别记为a和b，则函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+bx存在极值的概率为（　　）
    A．$\frac{13}{36}$B．$\frac{17}{36}$C．$\frac{19}{36}$D．$\frac{23}{36}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在?ABCD中，$\overrightarrow{AB}$•$\overrightarrow{BD}$=0，将△ABD沿BD折起，使平面ABD⊥平面BCD，2|$\overrightarrow{AB}$|2+|$\overrightarrow{BD}$|2=4，则三棱锥A-BCD的外接球的半径为（　　）
    A．1B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{2}}{4}$D．$\frac{1}{4}$

    查看答案和解析>>

    同步练习册答案