
| A. | $\frac{13}{36}$ | B. | $\frac{17}{36}$ | C. | $\frac{19}{36}$ | D. | $\frac{23}{36}$ |
分析 由题意求出f′(x),f(x)在R上存在极值点,则f′(x)=0有不等的两个实数根;△>0,求出满足条件的(a,b)共有几种情况,计算对应的概率值.
解答 解:由题意得:f′(x)=x2+ax+b,
若f(x)在R上存在极值点,则f′(x)=0有不等的两个实数根;
所以△=a2-4b>0,即a2>4b;
b=1时,a=3,4,5,6共4种;
b=2时,a=3,4,5,6共4种;
b=3时,a=4,5,6共3种;
b=4时,a=5,6共2种;
b=5时,a=5,6共2种;
b=6时,a=5,6共2种;
满足条件的(a,b)共4+4+3+2+2+2=17种情况,
所以函数f(x)在R上存在极值点的概率为P=$\frac{17}{36}$.
故选:B.
点评 本题考查了古典概型的概率计算问题,也考查了利用函数的导数判断函数极值的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{e}$ | B. | -e | C. | e | D. | $\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
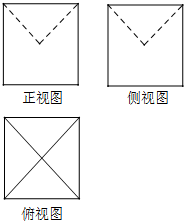 某几何体的三视图如图所示,图中的四边形都是边长为3的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为3的正方形,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{45}{2}$ | B. | $\frac{16}{3}$ | C. | 9-$\frac{π}{6}$ | D. | 27-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
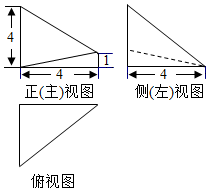 已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )
已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )| A. | $\frac{35}{3}$ | B. | 12 | C. | 16 | D. | $\frac{40}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 23 | C. | 32 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com