
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC= ![]() .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值.
科目:高中数学 来源: 题型:
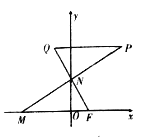
【题目】已知点![]() ,动点
,动点![]() ,
, ![]() 分别在
分别在![]() 轴,
轴, ![]() 轴上运动,
轴上运动, ![]() ,
, ![]() 为平面上一点,
为平面上一点, ![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() .
.
(Ⅰ)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点(直线
两点(直线![]() 不过
不过![]() ),交
),交![]() 于
于![]() ,
, ![]() 两点.若线段
两点.若线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() ,
, ![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,以x轴的非负半轴为极轴建立极坐标系,已知曲线C的参数方程为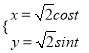 (t为参数)
(t为参数) 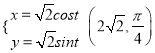 .
.
(1)若曲线C在点(1,1)处的切线为l,求l的极坐标方程;
(2)若点A的极坐标为![]() ,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的最小二乘法估计公式分别为:![]() =
=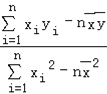 ,
,![]() =
=![]() ﹣
﹣![]()
![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
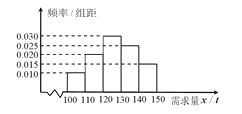
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin B=![]() b.
b.
(1)求角A的大小; (2)若a=6,b+c=8,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com