
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
分析 对任意x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2),说明对应的函数在(0,+∞)是一个减函数,故问题转化为判断四个函数单调性的问题,根据函数的解析式进行判断即可选出结论.
解答 解:因为对任意x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2),故满足条件的函数是一个减函数.
对于①,函数是反比例函数,其在(0,+∞)是一个减函数,满足题意;
对于②,f(x)=-|x|,其在(0,+∞)是一个减函数,满足题意;
对于③,函数是一次函数,其在(0,+∞)是一个减函数,满足题意;
对于④,函数f(x)=(x-1)2在(0,1)是减函数,在(1,+∞)上是增函数,故不满足题意;
故选A.
点评 本题考点是函数的单调性的判断与证明,考查根据已知的性质选择具有所给性质的函数的能力,在一些不要求证明函数单调性的函数单调性的判断中,常根据函数的解析式由那几个基本函数组成,综合利用这些基本函数的单调性来判断所研究函数的单调性.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
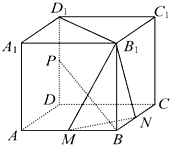 如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.
如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 公差为d的等差数列 | B. | 公差为cd的等差数列 | ||
| C. | 不是等差数列 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com