
分析 (1)根据集合的并集和补集交集的定义即可求出;
(2)根据集合与集合的关系,对B进行分类讨论.
解答 解:(1)∵若m=2,则B={x|-1≤x≤3},A={x|-2≤x≤4},
∴∁RB{x|x<-1或x>3},
∴A∪B={x|-2≤x≤4},
∴A∩(∁RB)={x|-2≤x<-1或3<x≤4},
(2)∵B⊆A,
当B=∅时满足题意,即-m+1>2m-1,解得m<$\frac{2}{3}$
当B≠∅时,则$\left\{\begin{array}{l}{-m+1≤2m-1}\\{-m+1≥-2}\\{2m-1≤4}\end{array}\right.$,
解得$\frac{2}{3}$≤m≤$\frac{5}{2}$,
综上所述m的取值范围为(-∞,$\frac{5}{2}$]
点评 本题主要考查了集合的包含关系判断及应用,以及集合关系中的参数取值问题,分类讨论思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [2,4) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
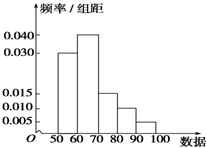 扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于80分的有参赛资格,80分以下(不包括80分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于80分的有参赛资格,80分以下(不包括80分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2016 | B. | 2016 | C. | 2018 | D. | -2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com