
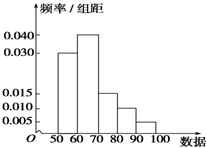
 扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于80分的有参赛资格,80分以下(不包括80分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于80分的有参赛资格,80分以下(不包括80分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:科目:高中数学 来源: 题型:选择题
| A. | 随机误差由解释变量和预报变量共同确定 | |
| B. | 预报变量只由解释变量确定 | |
| C. | 预报变量由解释变量和随机误差共同确定 | |
| D. | 随机误差只由预报变量确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4 | B. | $4\sqrt{2}$ | C. | 8 | D. | $4\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}π$ | B. | $4\sqrt{3}π$ | C. | $\frac{32π}{3}$ | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0” | |
| B. | “p∧q为真”是“p∨q为真”的必要不充分条件 | |
| C. | “若am2≤bm2,则a≤b”的否命题为真 | |
| D. | ?x∈R,sin2$\frac{x}{2}$+cos2$\frac{x}{2}$=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com