
分析 (1)通过$2{S_n}={3^n}+3$可知$2{a_n}=2{S_n}-2{S_{n-1}}={3^n}-{3^{n-1}}$,化简可知${a_n}={3^{n-1}}$,进而验证当n=1时是否成立即可;
(2)通过(1)即anbn=log3an可知当n>1时${b_n}={3^{1-n}}{log_3}{3^{n-1}}=({n-1})•{3^{1-n}}$,利用错位相减法计算可知${T_n}=\frac{13}{12}+\frac{6n+3}{{4×{3^n}}}$,进而检验当n=1时是否成立即可.
解答 解:(1)因为$2{S_n}={3^n}+3$,所以,2a1=3+3,故a1=3,
当n>1时,$2{S_{n-1}}={3^{n-1}}+3$,
此时,$2{a_n}=2{S_n}-2{S_{n-1}}={3^n}-{3^{n-1}}$,即${a_n}={3^{n-1}}$,
所以,${a_n}=\left\{{\begin{array}{l}{3,n=1}\\{{3^{n-1}},n>1}\end{array}}\right.$.
(2)因为anbn=log3an,所以${b_1}=\frac{1}{3}$,
当n>1时,${b_n}={3^{1-n}}{log_3}{3^{n-1}}=({n-1})•{3^{1-n}}$,
所以${T_1}={b_1}=\frac{1}{3}$,
当n>1时,${T_n}={b_1}+{b_2}+{b_3}+…+{b_n}=\frac{1}{3}+({1×{3^{-1}}+2×{3^{-2}}+…+({n-1}){3^{1-n}}})$.
所以$3{T_n}=1+({1×{3^0}+2×{3^{-1}}+…+({n-1}){3^{2-n}}})$,
两式相减,得$2{T_n}=\frac{2}{3}+({{3^0}+{3^{-1}}+{3^{2-n}}})-({n-1})•{3^{1-n}}=\frac{2}{3}+\frac{{1-{3^{1-n}}}}{{1-{3^{-1}}}}-({n-1})•{3^{1-n}}=\frac{13}{6}-\frac{6n+3}{{2×{3^n}}}$,
所以${T_n}=\frac{13}{12}+\frac{6n+3}{{4×{3^n}}}$,经检验,n=1时也适合,
综上可得:${T_n}=\frac{13}{12}+\frac{6n+3}{{4×{3^n}}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,考查分类讨论的思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
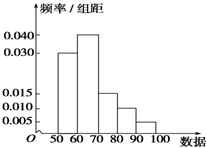 扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于80分的有参赛资格,80分以下(不包括80分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于80分的有参赛资格,80分以下(不包括80分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com