
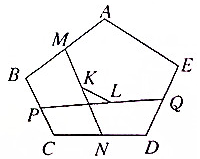
 如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.
如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$. 分析 通过连线,将多边形分割成三角形、四边形,为多个中点的利用创造条件,这是解本例的突破口.关键是做题中三角形中位线定理的运用.
解答 证明:连接BE,取其中点R,连接MR,RN,PR,PN,NQ,RQ.
∵点M是AB的中点,R是BE的中点,
∴MR∥AE,MR=$\frac{1}{2}$AE,
∵R,N、P、Q分别为BE、CD、BC、DE的中点,
连接CE,
∴PR∥CE,PR=$\frac{1}{2}$CE,NQ∥CE,NQ=$\frac{1}{2}$CE,
∴PR∥NQ,PR=NQ,
∴四边形PNQR是平行四边形,
∴RN与PQ互相平分,
∵点L是PQ的中点,
∴点L是RN的中点,
∵点K是MN的中点,
∴KL=$\frac{1}{2}$MR,
∴KL=$\frac{1}{4}$AE,
∴$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.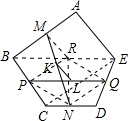
点评 此题主要考查平行四边形的判定与性质及三角形中位线定理的综合运用.注需要什么,构造什么,构造基本图形、构造线段的和差(倍分)关系、构造角的关系等,这是作辅助线的有效思考方法之一.


科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.1 | 3.9 | 4.5 |
| A. | 8 | B. | 8.5 | C. | 9 | D. | 9.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
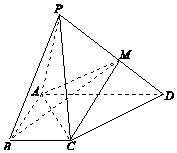 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠DAB=∠ABC=90°,AD=2BC,四棱锥P-ABCD的体积为10,点M在PD上.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠DAB=∠ABC=90°,AD=2BC,四棱锥P-ABCD的体积为10,点M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos2$\frac{α}{2}$ | B. | sin2$\frac{α}{2}$ | C. | cos2α | D. | sin2α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有一个内角小于60° | B. | 每一个内角都小于60° | ||
| C. | 有一个内角大于60° | D. | 每一个内角都大于60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com