

| A. | 3 | B. | 4 | C. | 5 | D. | 2$\sqrt{3}$ |
分析 根据题意,将|$\overrightarrow{AB}$+$\overrightarrow{AP}$|写成$\sqrt{(x-\frac{32}{5})^{2}+64-(\frac{32}{5})^{2}}$,其中x=$|\begin{array}{l}{\overrightarrow{BP}}\end{array}|$且x∈[0,5],再由二次函数的性质即可得结论.
解答 解:根据题意,可得|$\overrightarrow{AB}$+$\overrightarrow{AP}$|=$\sqrt{{|\begin{array}{l}{\overrightarrow{AB}+\overrightarrow{AB}+\overrightarrow{BP}}\end{array}|}^{2}}$
=$\sqrt{(2\overrightarrow{AB}+\overrightarrow{BP})^{2}}$
=$\sqrt{4{\overrightarrow{AB}}^{2}+4\overrightarrow{AB}•\overrightarrow{BP}+{\overrightarrow{BP}}^{2}}$
又矩形ABCD中,AB=4,AD=3,
设$|\begin{array}{l}{\overrightarrow{BP}}\end{array}|$=x,则x∈[0,5],
从而上式为$\sqrt{{x}^{2}-\frac{64}{5}x+64}$
=$\sqrt{(x-\frac{32}{5})^{2}+64-(\frac{32}{5})^{2}}$,
显然当x=5时,|$\overrightarrow{AB}$+$\overrightarrow{AP}$|取最小值为$\sqrt{(5-\frac{32}{5})^{2}+64-(\frac{32}{5})^{2}}$=5,
故选:C.
点评 本题考查平面向量模的最小值,将问题转化为二次函数问题是关键,属中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:选择题
函数 的定义域为
的定义域为 ,以下命题正确的是( )
,以下命题正确的是( )
①同一坐标系中,函数 与函数
与函数 的图象关于直线
的图象关于直线 对称;
对称;
②函数 的图象既关于点
的图象既关于点 成中心对称,对于任意
成中心对称,对于任意 ,又有
,又有 ,则
,则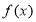 的图象关于直线
的图象关于直线 对称;
对称;
③函数 对于任意
对于任意 ,满足关系式
,满足关系式 ,则函数
,则函数 是奇函数.
是奇函数.
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4
在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com