
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,若T表示
,若T表示![]() 的内部及三边(含顶点)上的所有点的集合,则二元函数
的内部及三边(含顶点)上的所有点的集合,则二元函数![]() (点
(点![]() )的取值范围是____________。
)的取值范围是____________。
【答案】![]()
【解析】
把T划分为两个部分,分别讨论.
(1)当![]() ,即
,即![]() 时,
时,![]() .
.
设抛物线![]() 分别交边
分别交边![]() 于点
于点![]() ,点
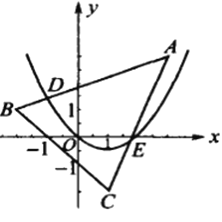
,点![]() 在曲边三角形ADE(DE是一段抛物线弧)上运动,如图.易知在点
在曲边三角形ADE(DE是一段抛物线弧)上运动,如图.易知在点![]() ,有
,有![]() .
.
由方程组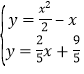 消去y整理得
消去y整理得![]() .
.
取小根![]() ,相应地
,相应地![]() ,故
,故![]() .
.
类似地有![]()
下面考虑直线![]() 是否与抛物线弧DE在T内相切.
是否与抛物线弧DE在T内相切.
为此由方程组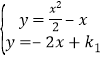 消去y得
消去y得![]() .令其判别式
.令其判别式![]() ;得
;得![]() .这时
.这时![]() ,此切点
,此切点![]() 在T的外部(线段AB的上方),所以直线
在T的外部(线段AB的上方),所以直线![]() 在T内不与抛物线弧DE相切.
在T内不与抛物线弧DE相切.
由以上可知![]() 在曲边三角形ADE上的最大值为9最小值为
在曲边三角形ADE上的最大值为9最小值为![]() .
.
(2)当![]() ,即
,即![]() 时,
时,![]() 点
点![]() 在曲边四边形BCED(ED是一段抛物线弧)上运动,如图.
在曲边四边形BCED(ED是一段抛物线弧)上运动,如图.
注意到抛物线![]() 开口向上,当
开口向上,当![]() 过点
过点![]() 时,
时,![]() 取最大值,从而,
取最大值,从而,![]() 取得最小值
取得最小值![]() .
.
当![]() 过B、C、E三点之一时,
过B、C、E三点之一时,![]() 取最小值,即
取最小值,即![]() 取得最大值
取得最大值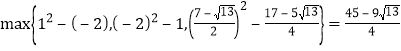 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 个数中一次随机地取
个数中一次随机地取![]() 个数,记所取的这
个数,记所取的这![]() 个数的和为
个数的和为![]() ,则下列说法错误的是( )
,则下列说法错误的是( )
A.事件“![]() ”的概率为
”的概率为![]()
B.事件“![]() ”的概率为
”的概率为![]()
C.事件“![]() ”与事件“
”与事件“![]() ”为互斥事件
”为互斥事件
D.事件“![]() ”与事件“
”与事件“![]() ”互为对立事件
”互为对立事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】称直角坐标系中纵横坐标均为整数的 点为“格点”,称一格点沿坐标线到原点的最短路程为该点到原点的“格点距离”,格点距离为定值的点的轨迹称为“格点圆”,该定值称为格点圆的半径,而每一条最短路程称为一条半径.当格点半径为2005时,格点圆的半径有________条.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列说法:①对于线性回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加5个单位;②在线性回归模型中,相关指数
平均增加5个单位;②在线性回归模型中,相关指数![]() 越接近于1,则模型回归效果越好;③两个随机变量的线性相关性越强,则相关系数就越接近1;④互斥事件不一定是对立事件,对立事件一定是互斥事件;⑤演绎推理是从特殊到一般的推理,它的一般模式是“三段论”.其中说法错误的个数为( )
越接近于1,则模型回归效果越好;③两个随机变量的线性相关性越强,则相关系数就越接近1;④互斥事件不一定是对立事件,对立事件一定是互斥事件;⑤演绎推理是从特殊到一般的推理,它的一般模式是“三段论”.其中说法错误的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网红直播平台为确定下一季度的广告投入计划,收集了近6个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
广告投入量/万元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/万元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
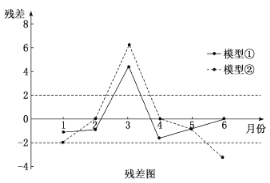
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由.
(2)残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除的异常数据是哪一组?
(ii)剔除异常数据后,求出(1)中所选模型的回归方程;
(iii)广告投入量![]() 时,(ii)中所得模型收益的预报值是多少?
时,(ii)中所得模型收益的预报值是多少?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: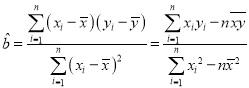 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图设计一幅矩形宣传画,要求画面面积为4840![]() ,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面高与宽的尺寸,才能使宣传画所用纸张面积最小?
,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面高与宽的尺寸,才能使宣传画所用纸张面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 和平面
和平面![]() :①若直线
:①若直线![]() 与平面
与平面![]() 内的无数条直线平行,则
内的无数条直线平行,则![]() ;②若直线
;②若直线![]() 与平面
与平面![]() 内的任意一条直线都不平行,则直线
内的任意一条直线都不平行,则直线![]() 和平面
和平面![]() 相交;③若
相交;③若![]() ,则直线
,则直线![]() 与平面
与平面![]() 内某些直线平行;④若
内某些直线平行;④若![]() ,则存在平面
,则存在平面![]() 内的直线
内的直线![]() ,使
,使![]() .以上结论中正确的个数为( )
.以上结论中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com