Question

【题目】某校高二理科1班共有50名学生参加学业水平模拟考试，成绩（单位：分，满分100分）大于或等于90分的为优秀，其中语文成绩近似服从正态分布，数学成绩的频率分布直方图如图.

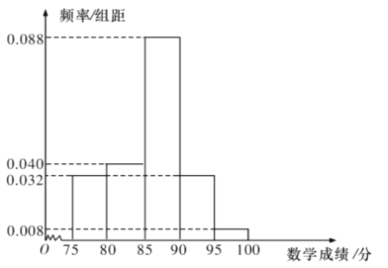
（1）这50名学生中本次考试语文、数学成绩优秀的大约各有多少人？

（2）如果语文和数学两科成绩都优秀的共有4人，从语文优秀或数学优秀的这些同学中随机抽取3人，设3人中两科都优秀的有X人，求X的分布列和数学期望；

（3）根据（1）（2）的数据，是否有99%以上的把握认为语文成绩优秀的同学，数学成绩也优秀？

	语文优秀	语文不优秀	合计
数学优秀
数学不优秀
合计

附：①若，则，；②；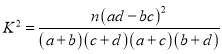

③

	0.1	0.05	0.025	0.010	p>0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1）语文成绩优秀的同学有人，数学成绩优秀的同学有人.（2）分布列见解析，；（3）没有以上的把握认为语文成绩优秀的同学，数学成绩也优秀.

【解析】

（1）语文成绩服从正态分布，根据正态分布的原则可得语文成绩优秀的概型及人数，根据数学成绩的频率分布直方图可以计算数学成绩优秀的概率及人数；

（2）语文和数学两科都优秀的有4人，则可算出单科优秀的学生人数，从中随机抽取3人，则3人中两科都优秀的可能为0、1、2、3四种情况，服从超几何分布，利用概率公式分别求出概率，即可写出分布列及数学期望；

（3）先完成列联表，利用公式求出卡方的值比较参考数据即可得出结论；

解：（1）因为语文成绩服从正态分布

所以语文成绩优秀的概率

数学成绩优秀的概率

所以语文成绩优秀的同学有人，

数学成绩优秀的同学有人.

（2）语文数学两科都优秀的有4人，单科优秀的有10人，的所有可能取值为0、1、2、3，

，，，

所以的分布列为：

（3）列联表：

	语文优秀	语文不优秀	合计
数学优秀
数学不优秀

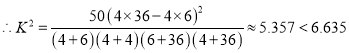
所以没有以上的把握认为语文成绩优秀的同学，数学成绩也优秀.