考点:平面与平面垂直的判定,平面与平面平行的判定,直线与平面垂直的判定
专题:作图题,证明题,空间位置关系与距离
分析:(1)取DD1的中点M,连结AM;从而证明HD1∥平面BDF,再证明B1H∥平面BDF,从而证明平面BDF∥平面B1D1H;
(2)连结OF,A1F,设正方体的棱长为a;则由勾股定理可证A1O⊥OF,再由BD⊥A1O可证A1O⊥平面BDF;
(3)由A1O⊥平面BDF,A1O?平面A1BD可证平面A1BD⊥平面BDF.
解答:
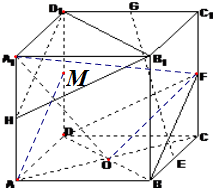
证明:(1)取DD
1的中点M,连结AM;
∵MF∥AB,MF=AB,
∴四边形ABFM是平行四边形,
∴AM∥BF,
又∵HD
1∥AM,
∴HD
1∥BF,
∴HD
1∥平面BDF,
同理可证,B
1H∥平面BDF,
又∵B
1H∩HD
1=H,
∴平面BDF∥平面B
1D
1H;
(2)连结OF,A
1F,设正方体的棱长为a;
则A
1O
2=a
2+
a2=
a
2,OF
2=
a
2+
a
2=
a
2;
A
1F
2=2a
2+
a
2=
a
2,
故A
1O⊥OF,
又∵BD⊥平面A
1C
1CA,A
1O?平面A
1C
1CA,
∴BD⊥A
1O,OF?平面BDF,BD?平面BDF
∴A
1O⊥平面BDF;
(3)∵A
1O⊥平面BDF,A
1O?平面A
1BD,
∴平面A
1BD⊥平面BDF.
点评:本题考查了面面平行的证明及线面、面面垂直的证明,注意作辅助线,属于中档题.

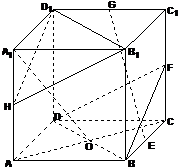 正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点.
正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点. 证明:(1)取DD1的中点M,连结AM;
证明:(1)取DD1的中点M,连结AM;

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 四棱锥A-BCDE的正视图和俯视图如图,其中正视图是等边三角形,俯视图是直角梯形.
四棱锥A-BCDE的正视图和俯视图如图,其中正视图是等边三角形,俯视图是直角梯形.