
【题目】已知函数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的极小值;
的极小值;
(2)已知函数![]() 在
在![]() 处取得极值,求证:
处取得极值,求证:![]() ;
;
(3)求函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() ;(2)见解析;(3)见解析;
;(2)见解析;(3)见解析;
【解析】
(1)当![]() 令
令 ![]() ,解得
,解得![]() .即可得出函数
.即可得出函数![]() 的单调性极值点.
的单调性极值点.
(2)![]() ,函数
,函数![]() 在
在![]() 处取得极值,可得
处取得极值,可得![]() ,解得:
,解得:![]() 或
或![]() 时,不满足条件,舍去,因此
时,不满足条件,舍去,因此![]() ,即可证明
,即可证明![]() .
.
(3)![]()
![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;
;
①![]() ,解得:
,解得:![]() ,此时
,此时![]() 有两个不相等的实数根
有两个不相等的实数根![]() .即函数
.即函数![]() 有两个极值点
有两个极值点![]() .设
.设![]() .对
.对![]() 与
与![]() 与0的大小关系即可得出函数零点的个数.②
与0的大小关系即可得出函数零点的个数.②![]() ,解得:
,解得:![]() 或
或![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上单调递增,即可得出函数
上单调递增,即可得出函数![]() 在
在![]() 上零点的个数.
上零点的个数.
(1)当![]() ,
,![]() .
.
![]() ,
,
令![]() ,解得
,解得![]() ,或
,或![]() ,
,
可得:函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 时函数
时函数![]() 取得极小值,
取得极小值,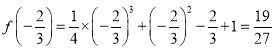 。
。
(2)![]() ,
,
∵函数![]() 在
在![]() 取得极值,
取得极值,
∴![]() ,
,
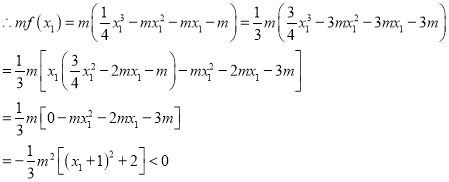
(3)![]() ,
,
![]() ,
,
![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;
;
①![]() ,解得:
,解得:![]() 或
或![]() ,此时
,此时![]() 有两个不相等的实数根
有两个不相等的实数根![]() .即函数
.即函数![]() 有两个极值点
有两个极值点![]() .设
.设![]() .
.
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上只有一个零点。
上只有一个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上有两个零点。
上有两个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上有三个零点。
上有三个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上有两个零点。
上有两个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上只有一个零点。
上只有一个零点。
②![]() ,解得:
,解得:![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;可得:函数
;可得:函数![]() 在
在![]() 上只有一个零点。
上只有一个零点。


科目:高中数学 来源: 题型:
【题目】![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问:在
两点,试问:在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?
恒成立?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
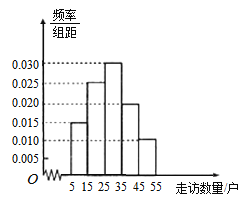
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个墙角,两墙面所成二面角的大小为![]() 有一块长为
有一块长为![]() 米,宽为
米,宽为![]() 米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓
米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓![]() .
.
(1)当![]() 为多少米时,储物仓底面三角形
为多少米时,储物仓底面三角形![]() 面积最大?
面积最大?
(2)当![]() 为多少米时,储物仓的容积最大?
为多少米时,储物仓的容积最大?
(3)求储物仓侧面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+sin x,x∈(-1,1),则满足f(a2-1)+f(a-1)>0的a的取值范围是( )
A. (0,2)B. (1,![]() )C. (1,2)D. (0,
)C. (1,2)D. (0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某互联网大会上,为了提升安全级别,将5名特警分配到3个重要路口执勤,每个人只能选择一个路口,每个路口最少1人,最多3人,且甲和乙不能安排在同一个路口,则不同的安排方法有( )
A. 180种 B. 150种 C. 96种 D. 114种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com