
| A. | $\frac{1}{32}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{128}$ | D. | $\frac{1}{2016}$ |
分析 依题意,可得f($\frac{1}{2}$)=f($\frac{1}{3}$)=$\frac{1}{2}$,再由当0≤x1<x2≤1时,有f(x1)≤f(x2),可得f($\frac{1}{{3}^{7}}$)=$\frac{1}{2}$f($\frac{1}{{3}^{6}}$)=$\frac{1}{{2}^{2}}$f($\frac{1}{{3}^{5}}$)=…=$\frac{1}{{2}^{7}}$f(1)=$\frac{1}{{2}^{7}}$=$\frac{1}{128}$,从而可得答案.
解答 ∵定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,$f(\frac{x}{3})=\frac{1}{2}f(x)$,
∴f(1)+f(0)=1,∴f(1)=1;
f($\frac{1}{2}$)+f(1-$\frac{1}{2}$)=1,∴f($\frac{1}{2}$)=$\frac{1}{2}$;
f($\frac{1}{3}$)=$\frac{1}{2}$f(1),
∴f($\frac{1}{2}$)=f($\frac{1}{3}$)=$\frac{1}{2}$;
∵$\frac{1}{1458}$>$\frac{1}{2016}$>$\frac{1}{2187}$,且当0≤x1<x2≤1时,有f(x1)≤f(x2),
∴f($\frac{1}{1458}$)<f($\frac{1}{2016}$)<f($\frac{1}{2187}$),
又∵f($\frac{1}{1458}$)=$\frac{1}{2}$f($\frac{1}{486}$)=$\frac{1}{{2}^{2}}$f(162)=…=$\frac{1}{{2}^{6}}$f($\frac{1}{2}$)=$\frac{1}{{2}^{7}}$=$\frac{1}{128}$.
f($\frac{1}{{3}^{7}}$)=$\frac{1}{2}$f($\frac{1}{{3}^{6}}$)=$\frac{1}{{2}^{2}}$f($\frac{1}{{3}^{5}}$)=…=$\frac{1}{{2}^{7}}$f(1)=$\frac{1}{{2}^{7}}$=$\frac{1}{128}$.
∴f($\frac{1}{2016}$)=$\frac{1}{{2}^{7}}$=$\frac{1}{128}$.
故选:C.
点评 本题考查抽象函数及其应用,突出考查赋值法,考查运算能力,属于难题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:存在x∈R,使cosx>1 | B. | ¬p:对任意x∈R,有cosx>1 | ||
| C. | ¬p:存在x∈R,使cosx≥1 | D. | ¬p:对任意x∈R,有cosx≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y-5=0 | B. | x+3y-1=0 | C. | 2x-y-3=0 | D. | x+3y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
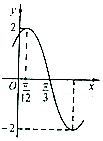 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)f(x)=Asin(ωx+φ)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)f(x)=Asin(ωx+φ)的部分图象如图所示,下列说法正确的是( )| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)的图象关于点$({-\frac{5π}{12},0})$对称 | |
| C. | 将函数f(x)的图象向左平移$\frac{π}{6}$个单位得到的函数图象关于y轴对称 | |
| D. | 函数f(x)的单调递增区间是$[{kπ+\frac{7π}{12},kπ+\frac{13π}{12}}],k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而非必要条件 | B. | 必要而非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com