
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
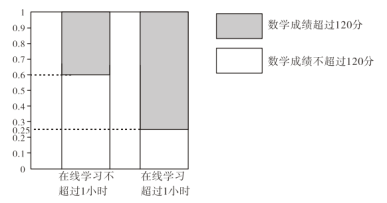
(Ⅰ)将频率视为概率,求学习时长不超过1小时但考试成绩超过120分的概率;
(Ⅱ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”.
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
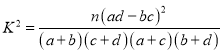
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,以下结论:
上的动点,以下结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③三棱锥![]() ,体积不变;
,体积不变;
④![]() 为
为![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大.
所成角最大.
其中正确的序号为( )
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
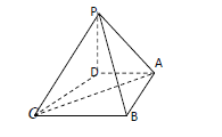
(1)在线段![]() 上是否存在一点F,使得
上是否存在一点F,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,试说明理由;
的值;若不存在,试说明理由;
(2)在(1)的条件下,若![]() 与
与![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若以该直角坐标系的原点为极点,
为参数),若以该直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() 为常数).
为常数).
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和
和![]() 有且仅有一个公共点,求
有且仅有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
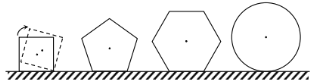
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个,在水平桌面上无滑动滚动一周,它们的中心的运动轨迹长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,….生数皆终,万物复苏,天以更元作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90至100),其余19人的年龄依次相差一岁,则年长者的年龄为( )
A.94B.95C.96D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
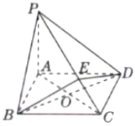
【题目】如图,在四棱锥![]() 中,ABCD为菱形,
中,ABCD为菱形,![]() 平面ABCD,连接AC,BD交于点O,
平面ABCD,连接AC,BD交于点O,![]() ,
,![]() ,E是棱PC上的动点,连接DE.
,E是棱PC上的动点,连接DE.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 面积的最小值是4时,求此时点E到底面ABCD的距离.
面积的最小值是4时,求此时点E到底面ABCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com