
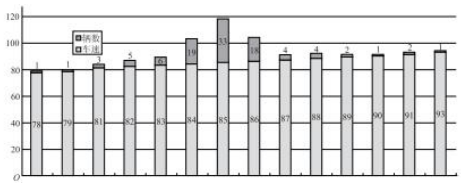
���� ��1�����¼�AΪ���Ӹÿ��ٳ��������г�������ȡ1�����ó�����������ٶȡ�����Ϊ��-3��=78.4����+2��=89.4������������ͼ�ɵ�����ĸ��ʣ�
��2�����¼�BΪ������������ȡ2����������2����������������ٶȡ��������֪��������Ϊ100����������ٶȸ���Ϊ5�����ɵ�������ʣ�
��3��������ٶȵĸ����ŷ��Ӷ���ֲ�����?��B$��2��\frac{1}{20}��$�����ɵó���
��� �⣺��1�����¼�AΪ���Ӹÿ��ٳ��������г�������ȡ1�����ó�����������ٶȡ���
����-3��=78.4����+2��=89.4��
����������ͼ��֪������ĸ���Ϊ$P��A��=P��x����-3�ң�+P��x����+2�ң�=P��x��78.4��+P��x��89.4��=\frac{1}{100}+\frac{4}{100}=\frac{1}{20}$��
��2�����¼�BΪ������������ȡ2����������2����������������ٶȡ�
�������֪��������Ϊ100����������ٶȸ���Ϊ5�������������Ϊ$P��B��=\frac{C_5^2}{{C_{100}^2}}=\frac{1}{495}$��
��3��������ٶȵĸ����ŷ��Ӷ���ֲ�����?��B$��2��\frac{1}{20}��$��
��$P����=0��=C_2^0{��\frac{1}{20}��^0}{��\frac{19}{20}��^2}=\frac{361}{400}$��$P����=1��=C_2^1{��\frac{1}{20}��^1}{��\frac{19}{20}��^1}=\frac{19}{200}$��$P����=2��=C_2^2{��\frac{1}{20}��^2}{��\frac{19}{20}��^0}=\frac{1}{400}$��
��˦ŵķֲ���Ϊ
| �� | 0 | 1 | 2 |
| P | $\frac{361}{400}$ | $\frac{19}{200}$ | $\frac{1}{400}$ |
���� ���⿼��������ͼ�����ʡ�����ֲ��е����ʼ�����ѧ�������ŵ���ʼ��㹫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{63}{32}$ | B�� | $\frac{31}{16}$ | C�� | $\frac{123}{64}$ | D�� | $\frac{127}{128}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪����f��x��=Asin����x+�գ�����A��0���أ�0��0���գ��У����䲿��ͼ����ͼ������f��x���Ľ���ʽΪ��������
��֪����f��x��=Asin����x+�գ�����A��0���أ�0��0���գ��У����䲿��ͼ����ͼ������f��x���Ľ���ʽΪ��������| A�� | $f��x��=2sin��{\frac{1}{2}x+\frac{��}{4}}��$ | B�� | $f��x��=2sin��{\frac{1}{2}x+\frac{3��}{4}}��$ | C�� | $f��x��=2sin��{\frac{1}{4}x+\frac{3��}{4}}��$ | D�� | $f��x��=2sin��{2x+\frac{��}{4}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{2}}}{4}$ | B�� | $\frac{{9\sqrt{2}}}{4}$ | C�� | $\frac{{3\sqrt{2}}}{2}$ | D�� | $\frac{{9\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
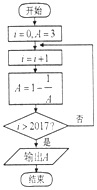 �Ķ���ͼ�ij����ͼ��������Ӧ�ij�������Ľ��Ϊ��������
�Ķ���ͼ�ij����ͼ��������Ӧ�ij�������Ľ��Ϊ��������| A�� | 3 | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com