练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．（$\frac{1}{\sqrt{x}}$-x2）10的展开式中x5的系数为210．

    分析 利用二项式展开式的通项公式，令x的指数等于5，求出r的值，再计算展开式中含x5项的系数．

    解答 解：（$\frac{1}{\sqrt{x}}$-x2）10的展开式中，通项公式为：
    Tr+1=${C}_{10}^{r}$•${（\frac{1}{\sqrt{x}}）}^{10-r}$•（-x2）r=（-1）r•${C}_{10}^{r}$•${x}^{\frac{5r}{2}-5}$，
    令$\frac{5r}{2}$-5=5，解得r=4；
    ∴展开式中含x5项的系数为（-1）4•${C}_{10}^{4}$=210．
    故答案为：210．

    点评 本题考查了二项式展开式通项公式的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．某市需对某环城快速车道进行限速，为了调研该道路车速情况，于某个时段随机对100辆车的速度进行取样，测量的车速制成如下条形图：

    经计算：样本的平均值μ=85，标准差σ=2.2，以频率值作为概率的估计值．已知车速过慢与过快都被认为是需矫正速度，现规定车速小于μ-3σ或车速大于μ+2σ是需矫正速度．
    （1）从该快速车道上所有车辆中任取1个，求该车辆是需矫正速度的概率；
    （2）从样本中任取2个车辆，求这2个车辆均是需矫正速度的概率；
    （3）从该快速车道上所有车辆中任取2个，记其中是需矫正速度的个数为ε，求ε的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$夹角为60°，且|$\overrightarrow{a}$|=2，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{7}$，则|$\overrightarrow{b}$|=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

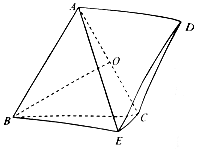    5．在多面体ABCDE中，平面ABC⊥平面BCE，四边形ABED为平行四边形，AB=AC=BC=2，CE=1，BE=$\sqrt{5}$，O为AC的中点．
    （1）求证：BO⊥AE；
    （2）求平面ABC与平面ACD所成锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．设等比数列{an}的前n项和为Sn，若S3，S9，S6成等差数列．且a2+a5=4，则a8的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

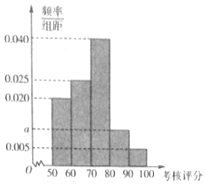    2．2016年，某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》，为了解本省各家企业对环保的重视情况，从中抽取了40家企业进行考核评分，考核评分均在[50，100]内，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图（满分为100分）．
    （Ⅰ）已知该省对本省每家企业每年的环保奖励y（单位：万元）与考核评分x的关系式为y=$\left\{\begin{array}{l}{-7，50≤x＜60}\\{0，60≤x＜70}\\{3，70≤x＜80}\\{6，80≤x＜100}\end{array}\right.$（负值为企业上缴的罚金），试估计该省在2016年对这40家企业投放环保奖励的平均值；
    （Ⅱ）在这40家企业中，从考核评分在80分以上（含80分）的企业中随机抽取2家企业座谈环保经验，求抽取的2家企业全部为考核评分在[80，90）内的企业的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知数列{an}满足an=$\left\{\begin{array}{l}{（\frac{1}{2}-a）n+1（n＜6）}\\{{a}^{n-5}（n≥6）}\end{array}\right.$若对于任意的n∈N*都有an＞an+1，则实数a的取值范围是（　　）
    A．（0，$\frac{1}{2}$）B．（$\frac{1}{2}$，$\frac{7}{12}$）C．（$\frac{1}{2}$，1）D．（$\frac{7}{12}$，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在等比数列{an}中，${a_3}=\frac{3}{2}，{S_3}=\frac{9}{2}$．
    （1）求数列{an}的通项公式；
    （2）设${b_n}={log_2}\frac{6}{{{a_{2n+1}}}}$，且{bn}为递增数列，若${c_n}=\frac{1}{{{b_n}^2}}$，求证：${c_1}+{c_2}+{c_3}+…+{c_n}＜\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．求下列函数的导数：
    （1）y=x3-cosx；
    （2）y=（3x2+2）（x-5）

    查看答案和解析>>

    同步练习册答案