
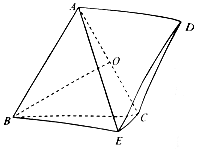
 在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.
在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.分析 (1)推导出BO⊥AC,BC⊥CE,则CE⊥平面ABC,从而CE⊥BO,进而BO⊥平面ACE,由此能证明BO⊥AE.
(2)以C为原点,CB为x轴,CE为y轴,建立空间直角坐标系C-xyz,利用向量法能求出平面ABC与平面ACD所成锐二面角的大小.
解答 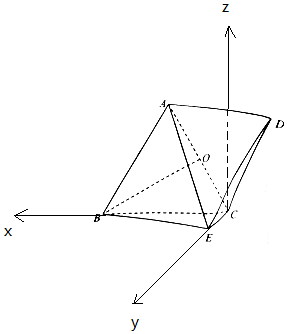 证明:(1)∵AB=AC=BC=2,
证明:(1)∵AB=AC=BC=2,
又O为AC中点,
∴BO⊥AC…(1分)
又$CE=1,BE=\sqrt{5},BC=2$,
∴BC2+CE2=BE2,∴BC⊥CE…(3分)
又∵平面ABC⊥平面BCE,
且平面ABC∩平面BCE=BC,
∴CE⊥平面ABC…(4分)
∴CE⊥BO,又CE∩AC=C,∴BO⊥平面ACE…(5分)
∵AE?平面ACE,∴BO⊥AE.…(6分)
解:(2)以C为原点,CB为x轴,CE为y轴,
建立空间直角坐标系C-xyz,
则$A({1,0,\sqrt{3}}),E({0,1,0}),B({2,0,0}),C({0,0,0})$…(7分)
∵$\overrightarrow{BA}=\overrightarrow{ED}∴\overrightarrow{CD}-\overrightarrow{CE}=({-1,0,\sqrt{3}}),\overrightarrow{CD}=({-1,1,\sqrt{3}})$…(8分)
由(1)知,$\overrightarrow{CE}=(0,1,0)$是平面ABC的平面角,
设平面ACD的法向量为$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{AD}=({-2,1,0})、\overrightarrow{CD}=({-1,1,\sqrt{3}})$
∴$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AD}=-2x+y=0\\ \overrightarrow n•\overrightarrow{CD}=-x+y+\sqrt{3}z=0\end{array}\right.$…(9分)
取x=1,得$\overrightarrow n=(1,2,-\frac{{\sqrt{3}}}{3})$…(10分)
设平面ABC与平面ACD所成锐二面角为θ,
则$cosθ=|{cos\left?{\overrightarrow n•\overrightarrow{CE}}\right>}|=\frac{{|{\overrightarrow n•\overrightarrow{CE}}|}}{{|{\overrightarrow n}||{\overrightarrow{CE}}|}}=\frac{{\sqrt{3}}}{2}$…(11分)
∴$θ=\frac{π}{6}$,∴平面ABC与平面ACD所成锐二面角的大小为$\frac{π}{6}$.…(12分)
点评 本题考查线线垂直的证明,考查二面角所成锐角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )| A. | $f(x)=2sin({\frac{1}{2}x+\frac{π}{4}})$ | B. | $f(x)=2sin({\frac{1}{2}x+\frac{3π}{4}})$ | C. | $f(x)=2sin({\frac{1}{4}x+\frac{3π}{4}})$ | D. | $f(x)=2sin({2x+\frac{π}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
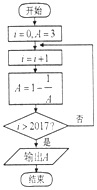 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | 3 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com