
分析 根据组合数公式求出n的值,再利用二项式展开式的通项公式求出展开式中含x5项的系数.
解答 解:${C}_{n}^{0}$+${C}_{n}^{1}$+…+${C}_{n}^{n}$=2n=256,
∴n=8;
∴${(x+\frac{1}{2\sqrt{x}})}^{8}$展开式中,通项公式为:
Tr+1=${C}_{8}^{r}$•x8-r•${(\frac{1}{2\sqrt{x}})}^{r}$=${(\frac{1}{2})}^{r}$•${C}_{8}^{r}$•${x}^{8-\frac{3}{2}r}$,
令8-$\frac{3}{2}$r=5,解得r=2;
∴展开式中含x5项的系数为${(\frac{1}{2})}^{2}$•${C}_{8}^{2}$=7.
故答案为:7.
点评 本题考查了组合数公式与二项式定理的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 运动员 | 比赛场次 | 总分 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| A | 3 | 2 | 2 | 2 | 4 | 2 | 6 | 21 | ||||
| B | 1 | 3 | 5 | 1 | 10 | 4 | 4 | 28 | ||||
| C | 9 | 8 | 6 | 1 | 1 | 1 | 2 | 28 | ||||
| D | 7 | 8 | 4 | 4 | 3 | 1 | 8 | 35 | ||||
| E | 3 | 12 | 5 | 8 | 2 | 7 | 5 | 42 | ||||
| F | 4 | 11 | 6 | 9 | 3 | 6 | 8 | 47 | ||||
| G | 10 | 12 | 12 | 8 | 12 | 10 | 7 | 71 | ||||
| H | 12 | 12 | 6 | 12 | 7 | 12 | 12 | 73 | ||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
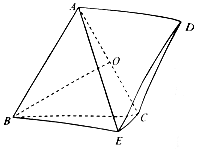 在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.
在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{7}{12}$) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{7}{12}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com