
| 运动员 | 比赛场次 | 总分 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| A | 3 | 2 | 2 | 2 | 4 | 2 | 6 | 21 | ||||
| B | 1 | 3 | 5 | 1 | 10 | 4 | 4 | 28 | ||||
| C | 9 | 8 | 6 | 1 | 1 | 1 | 2 | 28 | ||||
| D | 7 | 8 | 4 | 4 | 3 | 1 | 8 | 35 | ||||
| E | 3 | 12 | 5 | 8 | 2 | 7 | 5 | 42 | ||||
| F | 4 | 11 | 6 | 9 | 3 | 6 | 8 | 47 | ||||
| G | 10 | 12 | 12 | 8 | 12 | 10 | 7 | 71 | ||||
| H | 12 | 12 | 6 | 12 | 7 | 12 | 12 | 73 | ||||
分析 (1)由表格中的数据,我们可以分别求出运动员A和B前7场比赛积分的平均数和方差,作为度量两运动员比赛的成绩及稳定性的依据.从平均分和积分的方差来看,运动员A的平均积分及积分的方差都比运动员B的小,也就是说,在前7场比赛过程中,运动员A的成绩最为优秀,且表现也最为稳定.
(2)表中平均分低于6.5分的运动员共有5个,其中平均分低于5分的运动员有3个,平均分不低于5分且低于6.5分的运动员有职有2个,从这5个数据中任取2个,至少1个运动员平均分不低于5分的对立事件是取到的两人的平均分都低于5分,由此能求出至少1个运动员平均分不低于5分的概率.
(3)尽管此时还有4场比赛没有进行,但这里我们可以假设每位选手在各自的11场比赛中发挥的水平大致相同,因而可以把前7场比赛的成绩看作总体的一个样本,由此能求出结果.
解答 解:(1)由表格中的数据,我们可以分别求出运动员A和B前7场比赛积分的平均数和方差,
作为度量两运动员比赛的成绩及稳定性的依据.
运动员A的平均分$\overline{{x}_{1}}$=$\frac{1}{7}×21$=3,
方差${{S}_{1}}^{2}$=$\frac{1}{7}$[(3-3)2+(2-3)2+(2-3)2+(2-3)2+(2-3)2+(4-3)2+(6-3)2]=2;
运动员B的平均分$\overline{{x}_{2}}$=$\frac{1}{7}×28$=4,
方差${{S}_{2}}^{2}$=$\frac{1}{7}$[(1-4)2+(1-4)2+(3-4)2+(5-4)2+(10-4)2+(4-4)2+](4-4)2]=8,
从平均分和积分的方差来看,运动员A的平均积分及积分的方差都比运动员B的小,
也就是说,在前7场比赛过程中,运动员A的成绩最为优秀,且表现也最为稳定.
(2)表中平均分低于6.5分的运动员共有5个,其中平均分低于5分的运动员有3个,
平均分不低于5分且低于6.5分的运动员有职有2个,
从这5个数据中任取2个,基本事件总数n=${C}_{5}^{2}=10$,
至少1个运动员平均分不低于5分的对立事件是取到的两人的平均分都低于5分,
∴至少1个运动员平均分不低于5分的概率p=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$.
(3)尽管此时还有4场比赛没有进行,但这里我们可以假设每位选手在各自的11场比赛中发挥的水平大致相同,
因而可以把前7场比赛的成绩看作总体的一个样本,并由此估计每位运动员最后的成绩,
从已结束的7场比赛的积分来看,运动员A的成绩最为出色,而且表现最为稳定,
故预测A运动员获得最后的冠军,而运动员B和C平均分相同,但运动员C得分整体呈下降趋势,
所以预测运动员C将获得亚军.
点评 本题考查平均数、方差、古典概型等基本础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等,是基础题.


科目:高中数学 来源: 题型:选择题
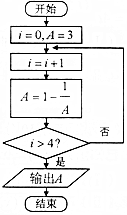 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
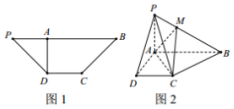 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
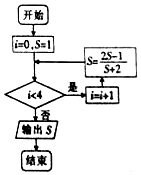 执行如图所示的程序框图,输出S的值为( )
执行如图所示的程序框图,输出S的值为( )| A. | -$\frac{31}{15}$ | B. | -$\frac{7}{5}$ | C. | -$\frac{31}{17}$ | D. | -$\frac{21}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 外语 | ||||
数学 | 优 | 良 | 及格 | |
| 优 | 8 | m | 9 | |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com