练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．三角形三个顶点是A（4，0），B（6，7），C（0，3）．
    （1）求BC边所在的直线的方程；
    （2）求△ABC的面积．

    分析 （1）求出直线BC的斜率，求出直线BC的方程即可；（2）求出A到BC的距离d，根据三角形的面积公式求出三角形的面积即可．

    解答 解：（1）${K_{BC}}=\frac{2}{3}，{l_{BC}}：2x-3y+9=0$．
    （2）A到BC的距离$d=\frac{{17\sqrt{13}}}{13}$，$|{BC}|=2\sqrt{13}$，
    故S=17．

    点评 本题考查了直线方程问题，考查三角形的面积公式，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．函数$f（x）=\sqrt{-{x^2}+4x+12}$的单调递增区间为[-2，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．${8^{-\frac{1}{3}}}+{log_3}$tan210°=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知实x，y数满足$\left\{\begin{array}{l}{y≤lnx}\\{x-2y-3≤0}\\{y+1≥0}\end{array}\right.$，则$z=\frac{y+1}{x}$的取值范围为[0，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

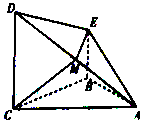    1．如图，在四棱锥A-BCDE中，CD⊥平面ABC，BE∥CD，AB=BC=CD，AB⊥BC，M为AD上一点，EM⊥平面ACD．
    （Ⅰ）证明：EM∥平面ABC；
    （Ⅱ）若CD=2，求四棱锥A-BCDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=2sinx+tanx-2x．
    （1）证明：函数f（x）在$（-\frac{π}{2}，\frac{π}{2}）$上单调递增；
    （2）若$x∈（0，\frac{π}{2}）$，f（x）＜mx2，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

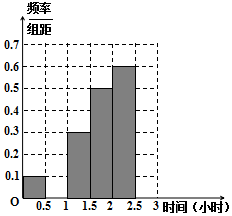    18．微信是现代生活进行信息交流的重要工具，随机对使用微信的60人进行了统计，得到如下数据统计表，每天使用微信时间在两小时以上的人被定义为“微信达人”，不超过两小时的人被定义为“非微信达人”．已知“非微信达人”与“微信达人”人数比恰为3：2．
    （Ⅰ）确定x，y，p，q的值，并补全频率分布直方图；
    （Ⅱ）为进一步了解使用微信对自己的日常工作和生活是否有影响，从“非微信达人”和“微信达人”60人中用分层抽样的方法确定5人，若需从这5人中随机选取2人进行问卷调查，求选取的2人中恰有1人为“微信达人”的概率． 
    使用微信时间
    （单位：小时）    		频数频率
    （0，0.5]30.05
    （0.5，1]xp
    （1，1.5]90.15
    （1.5，2]150.25
    （2，2.5]180.30
    （2.5，3]yq
    合计601.00

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在国际风帆比赛中，成绩以低分为优胜，比赛共11场，并以最佳的9场成绩计算最终的名次．在一次国际风帆比赛中，前7场比赛结束后，排名前8位的选手积分如表：
    运动员比赛场次 总分
    1234567891011
     A 32 22 4  2 6     21
     B 13 5 1 10 4 4     28 
     C 98 6 1 1 1 2     28 
     D 78 4 4 3 1 8     35 
     E3 12 5 8 2 7 5     42 
     F 4 116 9 3 6 8     47 
     G 1012 12 8 12 10 7     71 
     H12 12 6 12  7 12 12    73
    （1）根据表中的比赛数据，比较A与B的成绩及稳定情况；
    （2）从前7场平均分低于6.5的运动员中，随机抽取2个运动员进行兴奋剂检查，求至少1个运动员平均分不低于5分的概率．
    （3）请依据前7场比赛的数据，预测冠亚军选手，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知$f（x）=-\frac{1}{2}{x^2}+6x-8lnx$在[m，m+1]上不单调，则实数m的取值范围是（　　）
    A．（1，2）B．（3，4）C．（1，2]∪[3，4）D．（1，2）∪（3，4）

    查看答案和解析>>

    同步练习册答案