
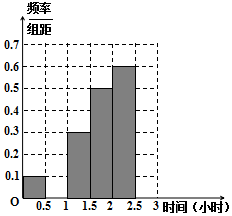
 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.| 使用微信时间 (单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
分析 (Ⅰ)由“非微信达人”与“微信达人”人数比恰为3:2,结合频率分布列和频率分布直方图,列出方程,能求出x,y,p,q的值,并能补全频率分布直方图.
(Ⅱ)选出的5人中,“微信达人”有2人,分别记为m,n,“非微信达人”有3人,分别记为a,b,c,由此得用列举法能求出选取的2人中恰有1人为“微信达人”的概率.
解答 解:(Ⅰ)“非微信达人”与“微信达人”人数比恰为3:2,
所以$\frac{3+x+9+15}{18+y}=\frac{3}{2}$,又3+x+9+15+18+y=60,(2分)
解这个方程组得$\left\{\begin{array}{l}x=9\\ y=6\end{array}\right.$,从而可得$\left\{\begin{array}{l}p=0.15\\ q=0.10\end{array}\right.$.(4分)
补全频率分布直方图如图所示:(6分)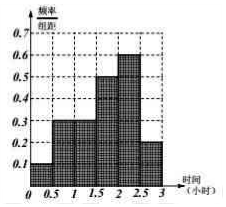
(Ⅱ)选出的5人中,“微信达人”有2人,分别记为m,n,
“非微信达人”有3人,分别记为a,b,c,(8分)
从中任选取2人的方法为:mn,ma,mb,mc,na,nb,nc,ab,ac,bc共有10种,
其中恰有1人为“微信达人”的方法为:ma,mb,mc,na,nb,nc有6种.(10分)
所以选取的2人中恰有1人为“微信达人”的概率$P=\frac{6}{10}=\frac{3}{5}$.(12分)
方法不一样,只要过程正确,答案准确给满分
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式、列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2loga8 | B. | 16 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
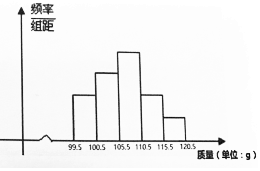 检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )
检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{30}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{60}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:$\root{3}{2}$:$\root{3}{3}$ | B. | 1:2:3 | C. | 1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$) | D. | 1:($\root{3}{2}$-1):($\root{3}{3}$-$\root{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
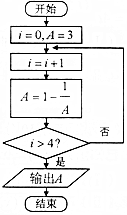 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
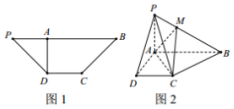 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
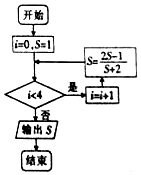 执行如图所示的程序框图,输出S的值为( )
执行如图所示的程序框图,输出S的值为( )| A. | -$\frac{31}{15}$ | B. | -$\frac{7}{5}$ | C. | -$\frac{31}{17}$ | D. | -$\frac{21}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
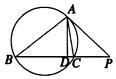 如图所示,PA切圆于A,PA=8,直线PCB交圆于C,B,连接AB,AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则$\frac{sinα}{sinβ}$的值等于( )
如图所示,PA切圆于A,PA=8,直线PCB交圆于C,B,连接AB,AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则$\frac{sinα}{sinβ}$的值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com