
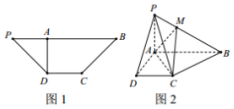
 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.分析 (1)连结BD,交AC于N,连结MN,推导出MN∥PD,由此能证明PD∥平面MAC.
(2)以A为原点,分别以AD,AB,AP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角M-AC-B的余弦值.
解答 证明:(1)连结BD,交AC于N,连结MN,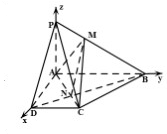
依题意知AB∥CD,∴△ABN~△CDN,∴$\frac{BN}{ND}=\frac{BA}{CD}=2$,
∵PM=$\frac{1}{2}$MB,∴$\frac{BN}{ND}=\frac{BM}{MP}=2$,
∴在△BPD中,MN∥PD,
又∵PD?平面MAC,MN?平面MAC,
∴PD∥平面MAC.
解:(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
PA⊥AD,PA?平面PAD,∴PA⊥平面PAD,
又AD⊥AB,从而PA,AD,AB两两垂直,
以A为原点,分别以AD,AB,AP为x,y,z轴,建立空间直角坐标系,
依题意AP=AD=1,AB=2,又PM=$\frac{1}{2}$MB,
∴A(0,0,0),B(0,2,0),P(0,0,1),M(0,$\frac{2}{3}$,$\frac{2}{3}$),C(1,1,0),
∴$\overrightarrow{AP}$=(0,0,1),$\overrightarrow{AM}$=(0,$\frac{2}{3},\frac{2}{3}$),$\overrightarrow{AC}$=(1,1,0),
∵PA⊥平面ABCD,∴$\overrightarrow{n}$=(0,0,1)是平面BAC的一个法向量,
设$\overrightarrow{m}$=(x,y,z)是平面MAC的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=\frac{2}{3}y+\frac{2}{3}z=0}\\{\overrightarrow{m}•\overrightarrow{AC}=x+y=0}\end{array}\right.$,取x=1,得$\overrightarrow{m}$=(1,-1,1),
设二面角M-AC-B的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
∴二面角M-AC-B的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查空间直线与直线、直线与平面的位置关系及二面角等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | .$y+4\sqrt{3}=3x$ | B. | .$y=x-\sqrt{3}$ | C. | $3y-3=\sqrt{3}x$ | D. | .$y-\sqrt{3}=\sqrt{3}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
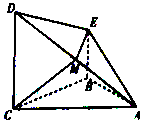 如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
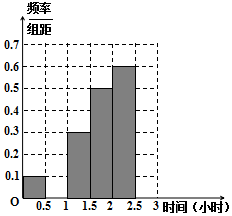 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.| 使用微信时间 (单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 50 | 200 | 100 | b | 50 | 500 |
| 频率 | 0.1 | a | 0.2 | c | 0.1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 运动员 | 比赛场次 | 总分 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| A | 3 | 2 | 2 | 2 | 4 | 2 | 6 | 21 | ||||
| B | 1 | 3 | 5 | 1 | 10 | 4 | 4 | 28 | ||||
| C | 9 | 8 | 6 | 1 | 1 | 1 | 2 | 28 | ||||
| D | 7 | 8 | 4 | 4 | 3 | 1 | 8 | 35 | ||||
| E | 3 | 12 | 5 | 8 | 2 | 7 | 5 | 42 | ||||
| F | 4 | 11 | 6 | 9 | 3 | 6 | 8 | 47 | ||||
| G | 10 | 12 | 12 | 8 | 12 | 10 | 7 | 71 | ||||
| H | 12 | 12 | 6 | 12 | 7 | 12 | 12 | 73 | ||||
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
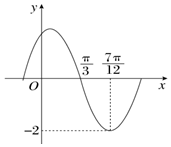 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com