练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
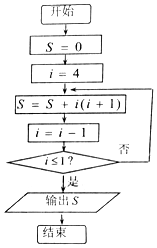
    2．执行如图所示的程序框图，则输出S的值为（　　）
    A．40B．38C．32D．20

    分析 根据流程图所示的顺序得出该程序的作用是累加并输出S=4×5+3×4+2×3的值．

    解答 解：分析程序中各变量、各语句的作用，
    再根据流程图所示的顺序，可知：
    该程序的作用是
    累加S=4×5+3×4+2×3的值，
    且S=4×5+3×4+2×3=38．
    故选：B．

    点评 本题考查了根据流程图写出程序运行结果的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知圆心为C的圆经过点A（1，1）和点B（2，-2）且圆心C在直线l：x+3y+3=0上．
    （1）求圆C的方程．
    （2）若P是直线3x+4y-21=0上的动点，PM，PN是圆C的两条切线，M，N为切点，设|PC|=t，把四边形PMCN的面积S表示为t的函数，并求出该函数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．锥体中，平行于底面的两个平面把锥体的体积三等分，这时高被分成三段的长自上而下的比为（　　）
    A．1：$\root{3}{2}$：$\root{3}{3}$B．1：2：3C．1：（$\sqrt{2}$-1）：（$\sqrt{3}$-$\sqrt{2}$）D．1：（$\root{3}{2}$-1）：（$\root{3}{3}$-$\root{3}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

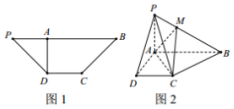    10．如图1，在等腰梯形PDCB中，PB∥DC，PB=3，DC=1，∠DPB=45°，DA⊥PB于点A，将△PAD沿AD折起，构成如图2所示的四棱锥P-ABCD，点M的棱PB上，且PM=$\frac{1}{2}$MB．
    （1）求证：PD||平面MAC；
    （2）若平面PAD⊥平面ABCD，求二面角M-AC-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知（2x+$\frac{1}{\sqrt{x}}$）n的展开式中的二项式系数之和为64，则展开式中的常数项为60（数字回答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

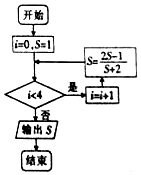    7．执行如图所示的程序框图，输出S的值为（　　）
    A．-$\frac{31}{15}$B．-$\frac{7}{5}$C．-$\frac{31}{17}$D．-$\frac{21}{17}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

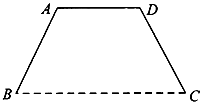    14．某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门BADC （如图），设计要求彩门的面积为S （单位：m2）•高为h（单位：m）（S，h为常数），彩门的下底BC固定在广场地面上，上底和两腰由不锈钢支架构成，设腰和下底的夹角为α，不锈钢支架的长度和记为l．
    （1）请将l表示成关于α的函数l=f（α）；
    （2）问当α为何值时l最小？并求最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．从1，3，5，7，9中任取3个数字，从2，4，6，8中任取2个数字，组成没有重复数字的五位数，则组成的五位数是偶数的概率是（　　）
    A．$\frac{2}{3}$B．$\frac{3}{5}$C．$\frac{1}{2}$D．$\frac{2}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．下列函数中既不是奇函数也不是偶函数的是（　　）
    A．y=2x+2-xB．y=lg$\frac{1}{x+1}$C．y=2|x|D．y=lg（x+$\sqrt{{x}^{2}+1}$）

    查看答案和解析>>

    同步练习册答案