
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 50 | 200 | 100 | b | 50 | 500 |
| 频率 | 0.1 | a | 0.2 | c | 0.1 | 1 |
分析 (1)由频率分布表能求出a,b,c.
(2)设“该户居民用水量不超过36吨”为事件A,由表能求出调查的500户居民中,用水量不超过36吨的概率.
(3)由用水量的频率分布表和题意,得居民该月用水费用的数据分组与频率分布表,由此能求出该市每户居民该月的平均水费.
解答 满分(12分)
解:(1)由频率分布表可得:
a=0.4,b=100,c=0.2.…(3分)
(2)设“该户居民用水量不超过36吨”为事件A,
由表可知,调查的500户居民中,用水量不超过36吨的概率为:
P(A)=0.1+0.4+0.2+0.2×$\frac{6}{10}$=0.82.…(7分)
(3)由用水量的频率分布表和题意,得居民该月用水费用的数据分组与频率分布表:
| 用水量(吨) | [0,10) | (10,20] | (20,30] | (30,40] | (40,50] |
| 用水费用 | [0,16] | (16,32] | (32,56] | (56,80] | (80,112] |
| 频率 | 0.1 | 0.4 | 0.2 | 0.2 | 0.1 |
点评 本题主要考查茎叶图、中位数、平均数、方差、古典概型等基础知识;考查学生应用意识、运算求解能力、数据处理能力及分析问题解决问题的能力;考查了分类与整合思想、必然与或然的数学思想.


科目:高中数学 来源: 题型:解答题
 已知f(x)为定义在R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=1,f(x)在x轴上的两个交点为(1,0)、(3,0).
已知f(x)为定义在R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=1,f(x)在x轴上的两个交点为(1,0)、(3,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:$\root{3}{2}$:$\root{3}{3}$ | B. | 1:2:3 | C. | 1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$) | D. | 1:($\root{3}{2}$-1):($\root{3}{3}$-$\root{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-∞,0) | C. | (-∞,0)∪(2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
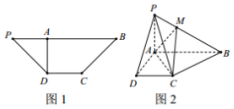 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
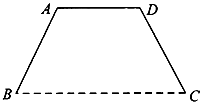 某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)•高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l.
某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)•高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com