
 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.分析 (Ⅰ)连接AC,BD交于点O,连接OP,则O为BD中点,说明∠PAO为AP与平面ABCD所成角,通过计算勾股定理证明AP⊥PH.结合PH⊥EF.证明PH⊥平面AEF.
(Ⅱ)证明AC⊥平面BDEF.求解${V_{A-BFED}}=\frac{1}{3}×{S_{BFED}}×|AO|=\frac{{2\sqrt{3}}}{3}$,推出点H到平面BFED的距离等于点C到平面BFED的距离,通过V=VA-BFED+VH-EFBD,求解即可
解答 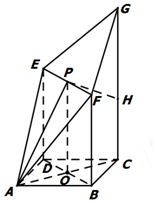 解:(1)连接AC,BD交于点O,连接OP,则O为BD中点,
解:(1)连接AC,BD交于点O,连接OP,则O为BD中点,
∴OP⊥DE∴OP⊥平面ABCD,
∴∠PAO为AP与平面ABCD所成角,∴∠PAO=60°.
在Rt△AOP中,$AO=1,OP=\sqrt{3},AP=2$∴$CG=\frac{{5\sqrt{3}}}{3},CH=\frac{{2\sqrt{3}}}{3}$.
在Rt△AHC中,$AH=\sqrt{A{C^2}+C{H^2}}=\frac{{4\sqrt{3}}}{3}$.
梯形OPHC中,$PH=\frac{{2\sqrt{3}}}{3}$.∴AP2+PH2=AH2
∴AP⊥PH.
又EH=FH,
∴PH⊥EF.
又AP∩EF=P,
∴PH⊥平面AEF.
(2)由(1)知,OP⊥平面ABCD,∴OP⊥AC.
又AC⊥BD,BD∩OP=O,∴AC⊥平面BDEF.∴${V_{A-BFED}}=\frac{1}{3}×{S_{BFED}}×|AO|=\frac{{2\sqrt{3}}}{3}$.
∵CG∥BF,BF?平面BFED,CG?平面BFED,∴CG∥平面BFED,
∴点H到平面BFED的距离等于点C到平面BFED的距离,
∴${V_{H-BFED}}=\frac{1}{3}×{S_{BFED}}×|CO|=\frac{{2\sqrt{3}}}{3}$.
$V={V_{A-BFED}}+{V_{H-EFBD}}=\frac{{4\sqrt{3}}}{3}$.
点评 本题考查直线与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力,转化思想的应用.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{-3+\sqrt{17}}}{2}$ | B. | $\frac{{3-\sqrt{17}}}{2}$ | C. | $\frac{{-3±\sqrt{17}}}{2}$ | D. | $\frac{{3±\sqrt{17}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
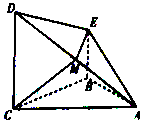 如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{11}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 50 | 200 | 100 | b | 50 | 500 |
| 频率 | 0.1 | a | 0.2 | c | 0.1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com