
分析 根据平面向量数量积运算与模长公式,列出方程解方程即可.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为60°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{7}$,
∴${(\overrightarrow{a}-2\overrightarrow{b})}^{2}$=${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=22-4×2×|$\overrightarrow{b}$|×cos60°+4${|\overrightarrow{b}|}^{2}$=28;
${|\overrightarrow{b}|}^{2}$-|$\overrightarrow{b}$|-6=0,
解得|$\overrightarrow{b}$|=3或|$\overrightarrow{b}$|=-2(不合题意,舍去);
∴|$\overrightarrow{b}$|=3.
故答案为:3.
点评 本题考查了平面向量数量积运算与模长公式的应用问题,是基础题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
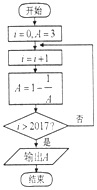 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | 3 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
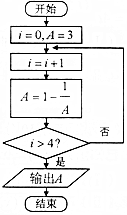 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com