练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
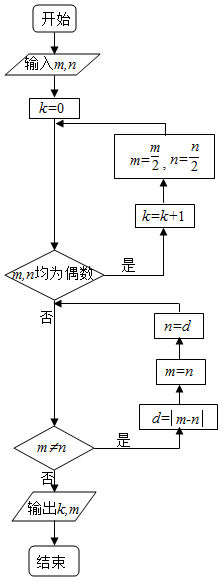
    13．执行如图所示的程序框图，如果输入的m=168，n=112，则输出的k，m的值分别为（　　）
    A．4，7B．4，56C．3，7D．3，56

    分析 模拟执行程序框图的运行过程，即可得出程序运行后输出的结果．

    解答 解：执行如图所示的程序框图，
    输入m=168，n=112，
    满足m、n都是偶数，k=1，m=84，n=56，
    满足m、n都是偶数，k=2，m=42，n=28，
    满足m、n都是偶数，k=3，m=21，n=14，
    不满足m、n都是偶数，
    满足m≠n，d=|m-n|=7，m=14，n=7，
    满足m≠n，d=|m-n|=7，m=7，n=7，
    不满足m≠n，退出循环，输出k=3，m=7．
    故选：C．

    点评 本题考查了程序框图的运行问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．一支田径运动队有男运动员64人，女运动员56人．现用分层抽样的方法，抽取若干人，若抽取的男运动员有8人，则抽取的女运动员人数为（　　）
    A．12B．8C．10D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

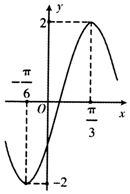    4．函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图所示，为了得到g（x）=Asinωx的图象，只需将函数y=f（x）的图象（　　）
    A．向左平移$\frac{π}{6}$个单位长度B．向左平移$\frac{π}{12}$个单位长度
    C．向右平移$\frac{π}{6}$个单位长度D．向右平移$\frac{π}{12}$个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知$\frac{2sinα+cosα}{sinα-cosα}$=3，则tan2α=$-\frac{8}{15}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$夹角为60°，且|$\overrightarrow{a}$|=2，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{7}$，则|$\overrightarrow{b}$|=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=|x-3|-2|x+1|的最大值为m．
    （1）求m的值和不等式f（x）＜1的解集；
    （2）若a，b∈（0，+∞），a2+2b2+c2=m，求ab+bc的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

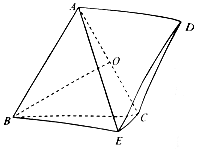    5．在多面体ABCDE中，平面ABC⊥平面BCE，四边形ABED为平行四边形，AB=AC=BC=2，CE=1，BE=$\sqrt{5}$，O为AC的中点．
    （1）求证：BO⊥AE；
    （2）求平面ABC与平面ACD所成锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

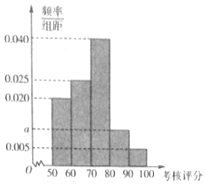    2．2016年，某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》，为了解本省各家企业对环保的重视情况，从中抽取了40家企业进行考核评分，考核评分均在[50，100]内，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图（满分为100分）．
    （Ⅰ）已知该省对本省每家企业每年的环保奖励y（单位：万元）与考核评分x的关系式为y=$\left\{\begin{array}{l}{-7，50≤x＜60}\\{0，60≤x＜70}\\{3，70≤x＜80}\\{6，80≤x＜100}\end{array}\right.$（负值为企业上缴的罚金），试估计该省在2016年对这40家企业投放环保奖励的平均值；
    （Ⅱ）在这40家企业中，从考核评分在80分以上（含80分）的企业中随机抽取2家企业座谈环保经验，求抽取的2家企业全部为考核评分在[80，90）内的企业的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在一次跳伞训练中，甲．乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“两位学员都没有降落在指定范围”可表示为（　　）
    A．（￢p）∨（￢q）B．p∨（￢q）C．p∨qD．（￢p）∧（￢q）

    查看答案和解析>>

    同步练习册答案