
分析 (1)分类讨论,求出函数的值域,即可求m的值;
( 2)由(1)知,a2+2b2+c2=4,利用基本不等式求ab+bc的最大值.
解答 解:(1)当x≤-1时,f(x)=(3-x)+2(x+1)=x+5≤4;
当-1<x<3时,f(x)=(3-x)-2(x+1)=-3x+1∈(-8,4);
当x≥3时,f(x)=(x-3)-2(x+1)=-x-5≤-8.…(3分)
故当x=-1时,f(x)取得最大值m=4;
|x-3|-2|x+1|<1,可化为
当x≤-1时,x+5<1,∴x<-4;当-1<x<3时,-3x+1<1,∴x>0,∴0<x<3;
当x≥3时,-x-5<1,∴x>-4,∴x≥3,
综上所述,不等式f(x)<1的解集为{x|x<-4或x>0};
(2)由(2)知,a2+2b2+c2=4,则ab+bc≤$\frac{1}{2}$[(a2+b2)+(b2+c2)]=2,
∴ab+bc的最大值为2.
点评 本题考查绝对值不等式,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
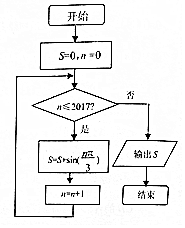 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | [1,2) | C. | [$\frac{1}{3}$,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x>x2 | B. | ?x∈R,ex<0 | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | ac2>bc2是a>b的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com