
| A. | (0,1] | B. | [1,2) | C. | [$\frac{1}{3}$,2) | D. | (2,+∞) |
分析 利用辅助角公式化简函数的解析式为函数f(x)=2sin(ωx+$\frac{π}{4}$),在区间(-$\frac{π}{3}$,$\frac{π}{4}$)上单调递增,即可$-\frac{π}{3}ω≥-\frac{3π}{4}+2kπ$且$\frac{π}{4}ω≤\frac{π}{4}+2kπ$,k∈Z,根据ω>0,可得ω的取值范围.
解答 解:函数f(x)=$\sqrt{2}$sinωx+$\sqrt{2}$cosωx(ω>0),
化简可得:f(x)=2sin(ωx+$\frac{π}{4}$),
∵在区间(-$\frac{π}{3}$,$\frac{π}{4}$)上单调递增,
∴$-\frac{π}{3}ω≥-\frac{3π}{4}+2kπ$且$\frac{π}{4}ω≤\frac{π}{4}+2kπ$,k∈Z,
解得:$\left\{\begin{array}{l}{ω≤\frac{9}{4}-6k}\\{ω≤1+8k}\end{array}\right.$k∈Z,
∵ω>0,
当k=0时,可得0<ω≤1,
故选A
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2},1})$ | B. | (-1,1)∪(1,2) | C. | (-∞,2) | D. | $[{-\frac{1}{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
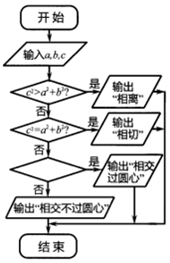 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )| A. | c=0? | B. | b=0? | C. | a=0? | D. | ab=0? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
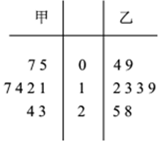 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
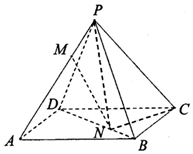 如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且$\frac{PM}{PA}$=$\frac{BN}{BD}$=$\frac{1}{3}$.
如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且$\frac{PM}{PA}$=$\frac{BN}{BD}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com