
分析 (1)讨论q=1,q≠1,由等比数列的通项公式和求和公式,解方程即可得到q,和a1,进而得到通项公式;
(2)由对数的运算性质,求得bn=2n,化cn≤$\frac{1}{4}$($\frac{1}{n-1}$-$\frac{1}{n}$),再由数列的求和方法:裂项相消求和,以及不等式的性质,即可得证.
解答 解:(1)∵${a_3}=\frac{3}{2},{S_3}=\frac{9}{2}$,
∴$\left\{{\begin{array}{l}{{S_3}-{a_3}={a_1}+{a_2}={a_1}({1+q})=3}\\{{a_3}={a_1}•q=\frac{3}{2}}\end{array}}\right.⇒\left\{{\begin{array}{l}{q=1}\\{{a_1}=\frac{3}{2}}\end{array}或\left\{{\begin{array}{l}{q=-\frac{1}{2}}\\{{a_1}=6}\end{array}}\right.}\right.$,
∴${a_n}=\frac{3}{2}或{a_n}=6•{({-\frac{1}{2}})^{n-1}}$.
(2)证明:由题意知${b_n}={log_2}\frac{6}{{{a_{2n+1}}}}={log_2}\frac{6}{{6•{{({-\frac{1}{2}})}^{2n}}}}={log_2}{2^{2n}}=2n$,
∴${c_n}=\frac{1}{{{b_n}^2}}=\frac{1}{{4{n^2}}}<\frac{1}{4n(n-1)}=\frac{1}{4}(\frac{1}{n-1}-\frac{1}{n})$,
∴${c_1}+{c_2}+{c_3}+…+{c_n}=\frac{1}{4}+\frac{1}{4}({1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n-1}-\frac{1}{n}})=\frac{1}{4}+\frac{1}{4}({1-\frac{1}{n}})=\frac{1}{2}-\frac{1}{4n}<\frac{1}{2}$.
点评 本题考查了等比数列的通项公式、前n项和公式,考查了分类讨论方法、和不等式的证明,注意运用裂项相消求和和不等式的性质,考查推理能力与计算能力,属于中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
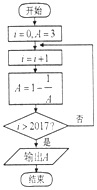 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | 3 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e0=1与ln 1=0 | B. | log39=2与9${\;}^{\frac{1}{2}}$=3 | ||
| C. | 8${\;}^{-\frac{1}{3}}$=$\frac{1}{2}$与log8$\frac{1}{2}$=-$\frac{1}{3}$ | D. | log77=1与71=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{3}+3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.
底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com