
分析 由题意可得α=kπ+$\frac{π}{12}$,k∈Z,代入要求的式子对k分奇数和偶数由诱导公式化简可得.
解答 解:∵tanα=tan$\frac{π}{12}$,∴α=kπ+$\frac{π}{12}$,k∈Z,
∴$\frac{cos(α-\frac{π}{12})}{sin(α+\frac{π}{12})}$=$\frac{coskπ}{sin(kπ+\frac{π}{6})}$,
当k为偶数时,$\frac{coskπ}{sin(kπ+\frac{π}{6})}$=$\frac{1}{\frac{1}{2}}$=2;
当k为奇数时,$\frac{coskπ}{sin(kπ+\frac{π}{6})}$=$\frac{-1}{-\frac{1}{2}}$=2
综上可得$\frac{cos(α-\frac{π}{12})}{sin(α+\frac{π}{12})}$=2,
故答案为:2.
点评 本题考查三角函数求值,涉及分类讨论的思想,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=sin(4x+$\frac{π}{3}$) | C. | y=sin(4x-$\frac{2π}{3}$) | D. | y=sin(x+$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
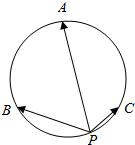 如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )
如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )| A. | (-1):2:3 | B. | (-3):2:1 | C. | (-2):3:6 | D. | (-6):3:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com