
分析 (1)列出当甲连胜2局或者乙连胜2局时,第二局比赛结束时比赛停止的概率求出p.(2)得出随机变量的所有可能取值,得出各自的概率从而得出分布列
解答 解:(1)依题意,当甲连胜2局或者乙连胜2局时,第二局比赛结束时比赛停止.∴${p}^{2}+(1-p)^{2}=\frac{5}{9}$.解得p=$\frac{2}{3}\\;\\;\\;或\\;p=\frac{1}{3}∵\\;p>\frac{1}{2}∴\\;p=\frac{2}{3}$.
(2)依题意知:X的所有可能值为2,4,6
设每两局比赛为1轮,则该轮结束时比赛停止的概率为$\frac{5}{9}$
若该轮结束时比赛还将继续,则甲乙在该轮中必是各得一分
此时该轮比赛结果对下轮比赛是否停止没有影响
从而有P(X=2)=$\frac{5}{9}$.
P(X=4)=(1-$\frac{5}{9}$)$\frac{5}{9}$=$\frac{20}{81}$
P(X=6)=1-$\frac{5}{9}$-$\frac{20}{81}$=$\frac{16}{81}$
∴随机变量X的分布列为:则随机变量ξ的分布列为:2
| X | 2 | 4 | 6 |
| P | $\frac{5}{9}$ | $\frac{20}{81}$ | $\frac{16}{81}$ |
点评 主要考查离散型随机变量的分布列和数学期望的求解方法,属于中档题型,在高考中经常反复考查.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,α⊥β,则m∥β | B. | 若m⊥n,n⊥β,则m∥β | ||
| C. | 若m⊥α,α⊥β,m与n异面,则n与β相交 | D. | 若m⊥α,n⊥β,m与n异面,则α与β相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
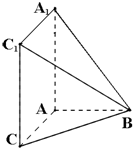 如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com