
分析 (1)判断函数f (x)在区间(0,+∞)上的单调性,并加以证明,先去绝对值号对函数表达式化简,根据其形式判断出函数的性质,再进行证明
(2)方程f(x)-kx2=0有四个不同的实数解,代入函数表达式,进行探究,由于方程带有绝对值,故需要分类去绝对值,在每一类中找出满足方程有两解的参数的值,合并既得.
解答 解:(1)函数f (x)的单调递增区间为[0,+∞),单调递减区间为(-∞,-1),(-1,0],证明如下:
∵f(x)=$\frac{|x|}{x+1}$,
∴当x≥0时,f(x)=1-$\frac{1}{x+1}$,
∵y=$\frac{1}{x+1}$在(0,+∞)上是减函数
∴f (x)在区间(0,+∞)上是增函数.
当x≤0时,f(x)=-1+$\frac{1}{x+1}$,
∵y=$\frac{1}{x+1}$在(-1,0]上是减函数,
∴f (x)在区间(-1,0]上是减函数
∵y=$\frac{1}{x+1}$在(-∞,-1)上是减函数,
∴f (x)在区间(-∞,-1)上是减函数.(4分)
(2)原方程即:$\frac{|x|}{x+1}$=kx2①
①由方程的形式可以看出,x=0恒为方程①的一个解.(5分)
②当x<0且x≠-1时方程①有解,则$\frac{-x}{x+1}$=kx2即kx2+kx+1=0,
当k=0时,方程kx2+kx+1=0无解;
当k≠0时,△=k2-4k≥0,即k<0或k≥4时,方程kx2+kx+1=0有解.
设方程kx2+kx+1=0的两个根分别是x1,x2则x1+x2=-1,x1x2=$\frac{1}{k}$.
当k>4时,方程kx2+kx+1=0有两个不等的负根;
当k=4时,方程kx2+kx+1=0有两个相等的负根;
当k<0时,方程kx2+kx+1=0有一个负根(8分)
③当x>0时,方程①有解,则$\frac{x}{x+1}$=kx2,kx2+kx-1=0
当k=0时,方程kx2+kx-1=0无解;
当k≠0时,△=k2+4k≥0即k>0或k≤-4时,方程kx2+kx-1=0有解.
设方程kx2+kx-1=0的两个根分别是x3,x4
∴x3+x4=-1,x3x4=-$\frac{1}{k}$,
∴当k>0时,方程kx2+2kx-1=0有一个正根,
当k≤-4时,方程kx2+2kx+1=0没有正根.(11分).
综上可得,当k∈(4,+∞)时,方程f (x)=kx2有四个不同的实数解.(13分).
点评 本题第一问考查单调性的判断,题目较易,第二问由方程有四个解来求参数的范围,本题对思维的严密性要求很高,需要熟练运用分类讨论的思想,因为题目中有太多的不确定性,本题难度较大.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
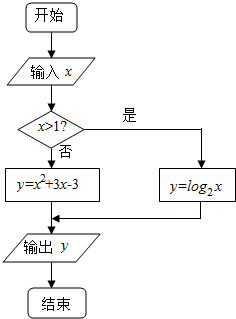
| A. | (-4,2]∪[2,+∞) | B. | [-4,1]∪[2,+∞) | C. | [-4,-2]∪{1}∪[4,+∞) | D. | (-∞,-4]∪{1}∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com