
【题目】已知函数![]() ,
,
(1)讨论![]() 在
在![]() 上的单调性.
上的单调性.
(2)当![]() 时,若
时,若![]() 在
在![]() 上的最大值为
上的最大值为![]() ,讨论:函数
,讨论:函数![]() 在
在![]() 内的零点个数.
内的零点个数.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减;(2)
上单调递减;(2)![]() 个零点
个零点
【解析】
(1)求得![]() ,根据
,根据![]() 范围可知
范围可知![]() ,进而通过对
,进而通过对![]() 的正负的讨论得到函数单调性;
的正负的讨论得到函数单调性;
(2)由(1)可得函数在![]() 上的单调性,进而利用最大值构造方程求得
上的单调性,进而利用最大值构造方程求得![]() ,得到函数解析式;利用单调性和零点存在定理可确定
,得到函数解析式;利用单调性和零点存在定理可确定![]() 在
在![]() 上有
上有![]() 个零点;令
个零点;令![]() ,求导后,可确定
,求导后,可确定![]() 在
在![]() 上存在零点,从而得到
上存在零点,从而得到![]() 的单调性,通过单调性和零点存在定理可确定零点个数.
的单调性,通过单调性和零点存在定理可确定零点个数.
(1)![]()
当![]() 时,
时,![]()
![]() 当
当![]() ,
,![]() 时,
时,![]() ;当
;当![]() ,
,![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减
上单调递减
(2)由(1)知,当![]() 时,
时,![]() 在
在![]() 上单调递增
上单调递增
![]() ,解得:
,解得:![]()
![]()
![]()
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]()
![]() 在
在![]() 内有且仅有
内有且仅有![]() 个零点
个零点
令![]() ,
,![]()
![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]()
![]() 在
在![]() 内单调递减
内单调递减
又![]() ,
,![]()
![]() ,使得
,使得![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
![]()
![]() 在
在![]() 上无零点且
上无零点且![]()
又![]()
![]() 在
在![]() 上有且仅有
上有且仅有![]() 个零点
个零点
综上所述:![]() 在
在![]() 上共有
上共有![]() 个零点
个零点


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
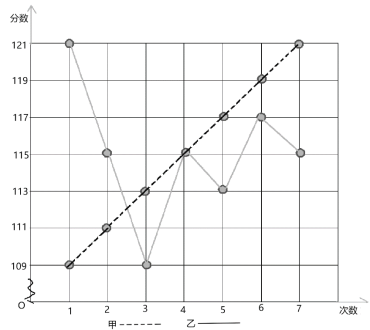
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为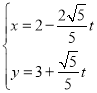 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求
.求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产量相同的机床一和机床二生产同一种零件,在一个小时内生产出的次品数分别记为![]() ,
,![]() ,它们的分布列分别如下:
,它们的分布列分别如下:
| 0 | 1 | 2 | 3 |
| 0.4 | 0.3 | 0.2 | 0.1 |
| 0 | 1 | 2 |
| 0.2 | 0.6 | 0.2 |
(1)哪台机床更好?请说明理由;
(2)记![]() 表示
表示![]() 台机床
台机床![]() 小时内共生产出的次品件数,求
小时内共生产出的次品件数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是边长为
是边长为![]() 的等边三角形,E、F分别为AB、AC的中点,
的等边三角形,E、F分别为AB、AC的中点,![]() ,沿EF把
,沿EF把![]() 折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥
折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥![]() 的外接球的表面积的最小值为________,此时四棱锥
的外接球的表面积的最小值为________,此时四棱锥![]() 的体积为________.
的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com