
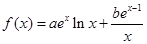 ,曲线
,曲线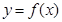 在点
在点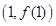 处的切线为
处的切线为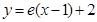 .
.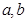 ;
;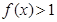 .
.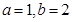 ;(2)详见解析.
;(2)详见解析.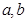 的值就一定要建立关于
的值就一定要建立关于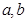 的两个方程,通过解方程求出
的两个方程,通过解方程求出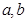 值,这就是方程思想,这里通过斜率关系确立一个方程,还有一个方程就是要用切点
值,这就是方程思想,这里通过斜率关系确立一个方程,还有一个方程就是要用切点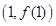 既在直线上,又在曲线上来确立,即用好切点的双重身份;(2)通过重新构造函数,利用导数知识来研究函数的极值和最值,进而达到证明不等式的目的,此题如果想直接去研究
既在直线上,又在曲线上来确立,即用好切点的双重身份;(2)通过重新构造函数,利用导数知识来研究函数的极值和最值,进而达到证明不等式的目的,此题如果想直接去研究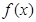 的最小值,通过最小值比
的最小值,通过最小值比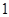 大,来达到证题的目的,那是很难办到的,所以说构造函数是需要功底的,也是需要技巧的.
大,来达到证题的目的,那是很难办到的,所以说构造函数是需要功底的,也是需要技巧的.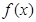 的定义域为
的定义域为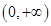 ,
,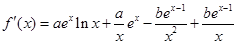 ,根据切点
,根据切点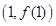 既在直线上,又在曲线上,依题意可得
既在直线上,又在曲线上,依题意可得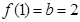 ,
,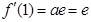 ,故
,故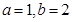 4分
4分 ,从而
,从而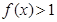 等价于
等价于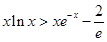 .
.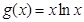 ,则
,则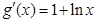 ,所以当
,所以当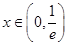 时,
时,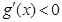 ,当
,当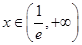 时,
时,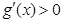 ,故
,故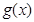 在
在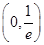 单调递减,在
单调递减,在 单调递增,从而
单调递增,从而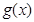 在
在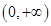 上的最小值为
上的最小值为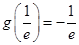 10分
10分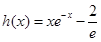 ,则
,则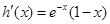 ,所以当
,所以当 时,
时,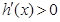 ,当
,当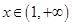 时,
时,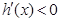 ,故
,故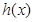 在
在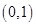 单调递增,在
单调递增,在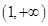 单调递减,从而
单调递减,从而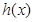 在
在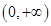 上的最大值为
上的最大值为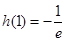 .又
.又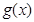 和
和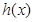 在
在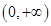 上取得最值的条件不同,所以综上:当
上取得最值的条件不同,所以综上:当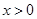 时,
时,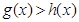 ,即
,即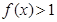 . 14分
. 14分

科目:高中数学 来源:不详 题型:解答题
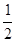
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).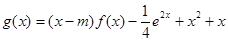 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
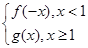 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| lim |
| x→0 |
| f(x+2)-f(2) |
| 2x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
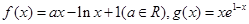 。
。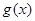 在区间
在区间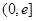 上的值域;
上的值域;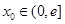 ,在区间
,在区间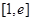 上都存在两个不同的
上都存在两个不同的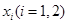 ,使得
,使得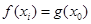 成立.若存在,求出a的取值范围;若不存在,请说明理由.
成立.若存在,求出a的取值范围;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com