
分析 由$\overrightarrow{CD}$2=($\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$)2=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$-2|$\overrightarrow{AC}$|$•|\overrightarrow{BD}|$•cosθ,能求出θ.
解答 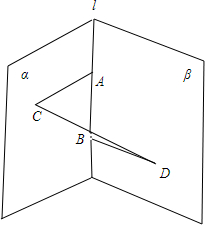 解:如图,∵二面角α-l-β的平面角为θ,AC⊥l,BD⊥l,
解:如图,∵二面角α-l-β的平面角为θ,AC⊥l,BD⊥l,
AB=AC=BD=1,CD=2,
∴$\overrightarrow{CD}$2=($\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$)2=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$-2|$\overrightarrow{AC}$|$•|\overrightarrow{BD}|$•cosθ,
∴4=1+1+1-2cosθ,解得cos$θ=-\frac{1}{2}$,
∴θ=120°.
故答案为:120°.
点评 本题考查二面角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 4 | C. | 3 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
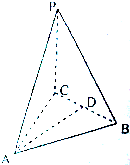 如图三棱锥P-ABC中,PC⊥平面ABC,PC=$\frac{2}{\sqrt{3}}$,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小.
如图三棱锥P-ABC中,PC⊥平面ABC,PC=$\frac{2}{\sqrt{3}}$,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 点P是边长为2的正△ABC的边BC的中点,将△ACP沿AP折起,使得二面角C-AP-B为直二面角,点M为线段AC的中点,点N在线段BC上,且BN=2NC.
点P是边长为2的正△ABC的边BC的中点,将△ACP沿AP折起,使得二面角C-AP-B为直二面角,点M为线段AC的中点,点N在线段BC上,且BN=2NC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
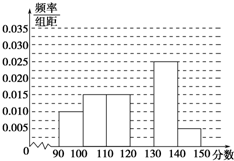 某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:| 数学成绩“优秀” | 数学成绩“一般” | 总计 | |
| 地理成绩“优秀” | 10 | 40 | 50 |
| 地理成绩“一般” | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com