
分析 在α内过O作OD⊥BC,连结AD,推导出BC⊥AD,从而∠ADO为二面角A-BC-O的平面角,解Rt△ADO,能求出结果.
解答 解:如图,在平面α内,过O作OD⊥BC,垂足为D,连结AD,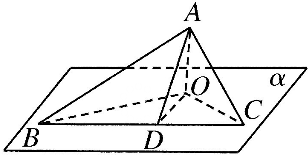
设OC=a,∵AO⊥α,BC?α,
∴AO⊥BC,又∵AO∩OD=O,∴BC⊥平面AOD,
∵AD?平面AOD,∴AD⊥BC,
∴∠ADO是二面角A-BC-O的平面角,
∵AO⊥α,OB?α,OC?α,∴AO⊥OB,AO⊥OC,
又∠ABO=30°,∠ACO=45°,∴AO=a,AC=$\sqrt{2}a$,AB=2a,
在Rt△ABC中,∠BAC=90°,
∴BC=$\sqrt{A{C}^{2}+A{B}^{2}}=\sqrt{6}a$,∴AD=$\frac{AB•AC}{BC}$=$\frac{2a•\sqrt{2}a}{\sqrt{6}a}$=$\frac{2\sqrt{3}}{3}a$,
在Rt△AOD中,sin∠ADO=$\frac{AO}{AD}=\frac{a}{\frac{2\sqrt{3}}{3}a}$=$\frac{\sqrt{3}}{2}$,
∴∠ADO=60°.
∴二面角A-BC-O的大小是60°.
点评 本题考查二面角的求法,是中档题,解题基本步骤为“一作二证三求”,解题时要注意顶点位置的合理选择.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
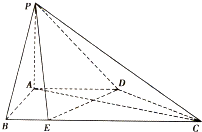 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,PA⊥AB,AD∥BC,AB⊥AD,点E在BC上,BC=2AB=2AD=4BE=4.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,PA⊥AB,AD∥BC,AB⊥AD,点E在BC上,BC=2AB=2AD=4BE=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,侧棱BB1与底面ABC所成的角为$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,侧棱BB1与底面ABC所成的角为$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正三棱柱ABC-A1B1C1中,点D是棱AB的中点,BC=1,AA1=$\sqrt{3}$.
如图,在正三棱柱ABC-A1B1C1中,点D是棱AB的中点,BC=1,AA1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
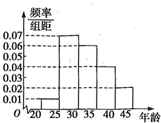 2015年10月29日夜里,全面放开二胎的消息一公布,迅速成为人们热议的热点,为此,某网站进行了一次民意调查,参与调查的网民中,年龄分布情况如图所示:
2015年10月29日夜里,全面放开二胎的消息一公布,迅速成为人们热议的热点,为此,某网站进行了一次民意调查,参与调查的网民中,年龄分布情况如图所示:| 计划要二胎 | 不计划要二胎 | 合计 | |
| 30岁以下 | |||
| 不低于30岁 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com