
 2015��10��29��ҹ�ȫ��ſ���̥����Ϣһ������Ѹ�ٳ�Ϊ����������ȵ㣬Ϊ�ˣ�ij��վ������һ��������飬�������������У�����ֲ������ͼ��ʾ��
2015��10��29��ҹ�ȫ��ſ���̥����Ϣһ������Ѹ�ٳ�Ϊ����������ȵ㣬Ϊ�ˣ�ij��վ������һ��������飬�������������У�����ֲ������ͼ��ʾ��| �ƻ�Ҫ��̥ | ���ƻ�Ҫ��̥ | �ϼ� | |
| 30������ | |||
| ������30�� | |||
| �ϼ� |
| P��K2��k0�� | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
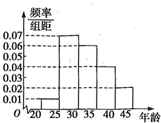
���� ��1����Ƶ�ʷֲ�ֱ��ͼ����֪����ǡ����[30��40��֮��ĸ���Ϊ��0.06+0.04����5=0.5��
��2����Ƶ�ʷֲ�ֱ��ͼ�����2��2�����������K2�����ٽ�ֵ���ȶԣ����ɵõ�û��90%���ϵİ�����Ϊ�ƻ�Ҫ��̥�������йأ���
��� �⣺��1����Ƶ�ʷֱ�ֱ��ͼ��֪�������ȡ1�ˣ�
������ǡ����[30��40��֮��ĸ���Ϊ��0.06+0.04����5=0.5��
��2���ٸ��ݷֲ������������30�����µ�����Ӧ��ȡ40�ˣ�
���ܵ���30�������Ӧ��ȡ60�ˣ�
��2��2���������£�
| �ƻ�Ҫ��̥ | ���ƻ�Ҫ��̥ | �ϼ� | |
| 30������ | 25 | 15 | 40 |
| ������30�� | 30 | 30 | 60 |
| �ϼ� | 55 | 45 | 100 |
���� ���⿼������Լ����Ӧ�ã�����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�����������������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 108 | B�� | 96 | C�� | 120 | D�� | 112 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
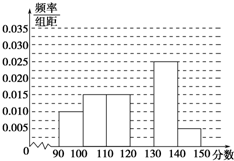 ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ100��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����[90��100����[100��110��������[140��150]��õ���ͼ����Ƶ�ʷֲ�ֱ��ͼ�����гɼ���[130��150]�ij�Ϊ�����㡱�������ij�Ϊ��һ�㡱���۲�ͼ�ε���Ϣ���ش��������⣺
ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ100��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����[90��100����[100��110��������[140��150]��õ���ͼ����Ƶ�ʷֲ�ֱ��ͼ�����гɼ���[130��150]�ij�Ϊ�����㡱�������ij�Ϊ��һ�㡱���۲�ͼ�ε���Ϣ���ش��������⣺| ��ѧ�ɼ������㡱 | ��ѧ�ɼ���һ�㡱 | �ܼ� | |
| �����ɼ������㡱 | 10 | 40 | 50 |
| �����ɼ���һ�㡱 | 20 | 30 | 50 |
| �ܼ� | 30 | 70 | 100 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-$\frac{1}{3}$��3�� | B�� | ��-�ޣ�-$\frac{1}{3}}$���ȣ�3��+�ޣ� | C�� | ��-�ޣ�-3���ȣ�${\frac{1}{3}$��+�ޣ� | D�� | ��-3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
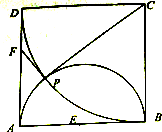 ��ͼ���ı���ABCDΪ�����Σ���ABΪֱ�� �İ�ԲE����CΪԲ��CBΪ�뾶��Բ���ཻ�ڵ�P������P��ԲC������PF��AD�ڵ�F������CP��
��ͼ���ı���ABCDΪ�����Σ���ABΪֱ�� �İ�ԲE����CΪԲ��CBΪ�뾶��Բ���ཻ�ڵ�P������P��ԲC������PF��AD�ڵ�F������CP���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com