
分析 (1)利用新定义得到ab的方程,利用离心率以及椭圆中a、b、c的关系,求解a,b即可得到椭圆的方程.
(2)①当k=0时,-1<m<1②当k≠0时,联立$\left\{\begin{array}{l}\frac{x^2}{3}+{y^2}=1\\ y=kx+m\end{array}\right.$,消去y,利用判别式,推出m2<1+3k2,设P(x1,y1),Q(x2,y2),PQ的中点R(x0,y0)利用韦达定理求出中点坐标,当|AP|=|AQ|时,点A,R在PQ的中垂线上,求出PQ的中垂线方程为:$y=-\frac{1}{k}x-1$,代入得到2m=3k2+1,然后求解m的范围.
解答 解:(1)由题意可得:M(0,b),N(a,0),
∴$\overrightarrow{OM}?\overrightarrow{ON}=|\overrightarrow{OM}||\overrightarrow{ON}|sin\frac{π}{2}=ab=\sqrt{3}$,
又$e=\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,且a2=b2+c2,
∴a2=3,b2=1,
∴椭圆C的方程为:$\frac{x^2}{3}+{y^2}=1$.
(2)由条件知A(0,-1)为椭圆下顶点
①当k=0时,-1<m<1;
②当k≠0时,联立$\left\{\begin{array}{l}\frac{x^2}{3}+{y^2}=1\\ y=kx+m\end{array}\right.$,消去y可得:(3k2+1)x2+6kmx+3m2-3=0,
∴△=36k2m2-4(3k2+1)(3m2-3)>0
∴m2<1+3k2
设P(x1,y1),Q(x2,y2),PQ的中点R(x0,y0)
∴${x_1}+{x_2}=-\frac{6km}{{3{k^2}+1}}$,${x_1}{x_2}=\frac{{3{m^2}-3}}{{3{k^2}+1}}$
∴${x_0}=\frac{{{x_1}+{x_2}}}{2}=-\frac{3km}{{3{k^2}+1}}$${y_0}=k{x_0}+m=\frac{m}{{3{k^2}+1}}$,即$R(-\frac{3km}{{3{k^2}+1}},\frac{m}{{3{k^2}+1}})$
当|AP|=|AQ|时,点A,R在PQ的中垂线上
据题意可得PQ的中垂线方程为:$y=-\frac{1}{k}x-1$
∴$\frac{m}{{3{k^2}+1}}=-\frac{1}{k}•(-\frac{3km}{{3{k^2}+1}})-1$
∴2m=3k2+1
故$\left\{\begin{array}{l}{m^2}<2m\\ 2m>1\end{array}\right.$,∴$\frac{1}{2}<m<2$
综上m的范围是(-1,2).
点评 本题考查直线与椭圆的位置关系的综合应用,范围问题的求解的方法,设而不求的方法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
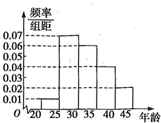 2015年10月29日夜里,全面放开二胎的消息一公布,迅速成为人们热议的热点,为此,某网站进行了一次民意调查,参与调查的网民中,年龄分布情况如图所示:
2015年10月29日夜里,全面放开二胎的消息一公布,迅速成为人们热议的热点,为此,某网站进行了一次民意调查,参与调查的网民中,年龄分布情况如图所示:| 计划要二胎 | 不计划要二胎 | 合计 | |
| 30岁以下 | |||
| 不低于30岁 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,x02+1<0”的否定是“?x0∈R,x02+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 若f(x)是R上的偶函数,则f(x+1)的图象的对称轴是x=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
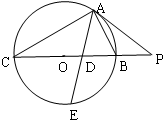 如图,△ABC内接于直径为BC的圆O,过点作圆O的切线交CB的延长线于点P,AE交BC和圆O于点D、E,且$\frac{AC}{AB}$=$\frac{CD}{DB}$,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点作圆O的切线交CB的延长线于点P,AE交BC和圆O于点D、E,且$\frac{AC}{AB}$=$\frac{CD}{DB}$,若PA=2PB=10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com