
分析 根据椭圆的定义,可以设|PF1|=m,|PF2|=n,在△PF1F2中,根据余弦定理,结合${S}_{{{△F}_{1}PF}_{2}}$=$\frac{1}{2}$mn•sin60°,列出方程即可求出b的值.
解答 解:根据椭圆的定义,设|PF1|=m,|PF2|=n,则
在△PF1F2中,根据余弦定理得,
cos60°=$\frac{{m}^{2}{+n}^{2}-{4c}^{2}}{2mn}$=$\frac{{(m+n)}^{2}-{4c}^{2}-2mn}{2mn}$
即$\frac{1}{2}$=$\frac{{4a}^{2}-{4c}^{2}-2mn}{2mn}$,
所以3mn=4a2-4c2=4b2;
又${S}_{△{{PF}_{1}F}_{2}}$=$\frac{1}{2}$mn•sin60°=$\frac{\sqrt{3}}{4}$mn=$\frac{\sqrt{3}}{4}$•$\frac{4}{3}$b2
=$\frac{\sqrt{3}}{3}$b2=12$\sqrt{3}$,
解得b2=36,
所以b=6.
故答案为:6.
点评 本题重点考查了椭圆的定义与性质的应用问题,也考查了正弦、余弦定理的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{6}$ | B. | -6 | C. | 6 | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2e2] | B. | [0,2e3] | C. | (0,2e2] | D. | (0,2e3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
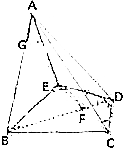 如图所示,在四棱锥A-BCDE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE,又AE=BE=2,∠CDE=120°,
如图所示,在四棱锥A-BCDE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE,又AE=BE=2,∠CDE=120°,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
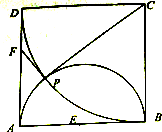 如图,四边形ABCD为正方形,以AB为直径 的半圆E与以C为圆心CB为半径的圆弧相交于点P,过点P作圆C的切线PF交AD于点F,连接CP.
如图,四边形ABCD为正方形,以AB为直径 的半圆E与以C为圆心CB为半径的圆弧相交于点P,过点P作圆C的切线PF交AD于点F,连接CP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com