
| A. | [0,2e2] | B. | [0,2e3] | C. | (0,2e2] | D. | (0,2e3] |
分析 求得f(-1),由题意可得alnx-x2-2≤-2+a在x>0恒成立,讨论x的范围,分x=e,0<x<e,x>e,运用参数分离和构造函数,求得导数和单调区间,可得最值,进而得到a的范围.
解答 解:由f(-1)=-2+a,可得alnx-x2-2≤-2+a在x>0恒成立,
即为a(1-lnx)≥-x2,
当x=e时,0>-e2显然成立;
当0<x<e时,有1-lnx>0,可得a≥$\frac{{x}^{2}}{lnx-1}$,
设g(x)=$\frac{{x}^{2}}{lnx-1}$,0<x<e,
g′(x)=$\frac{2x(lnx-1)-x}{(lnx-1)^{2}}$=$\frac{x(2lnx-3)}{(lnx-1)^{2}}$,
由0<x<e时,2lnx<2<3,则g′(x)<0,g(x)在(0,e)递减,
且g(x)<0,
可得a≥0;
当x>e时,有1-lnx<0,可得a≤$\frac{{x}^{2}}{lnx-1}$,
设g(x)=$\frac{{x}^{2}}{lnx-1}$,x>e,
g′(x)=$\frac{2x(lnx-1)-x}{(lnx-1)^{2}}$=$\frac{x(2lnx-3)}{(lnx-1)^{2}}$,
由e<x<e${\;}^{\frac{3}{2}}$时,g′(x)<0,g(x)在(e,e${\;}^{\frac{3}{2}}$)递减,
由x>e${\;}^{\frac{3}{2}}$时,g′(x)>0,g(x)在(e${\;}^{\frac{3}{2}}$,+∞)递增,
即有g(x)在x=e${\;}^{\frac{3}{2}}$处取得极小值,且为最小值2e3,
可得a≤2e3,
综上可得0≤a≤2e3.
故选:B.
点评 本题考查函数的最值的求法和应用,注意运用参数分离和分类讨论的思想方法,以及构造函数法,求出导数和最值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人紧急转移安置,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离路率市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成(0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率直方图:
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人紧急转移安置,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离路率市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成(0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率直方图:| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | a=30 | b | |
| 捐款不超过500元 | c | d=6 | |
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,x02+1<0”的否定是“?x0∈R,x02+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 若f(x)是R上的偶函数,则f(x+1)的图象的对称轴是x=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
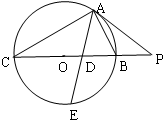 如图,△ABC内接于直径为BC的圆O,过点作圆O的切线交CB的延长线于点P,AE交BC和圆O于点D、E,且$\frac{AC}{AB}$=$\frac{CD}{DB}$,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点作圆O的切线交CB的延长线于点P,AE交BC和圆O于点D、E,且$\frac{AC}{AB}$=$\frac{CD}{DB}$,若PA=2PB=10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-$\frac{π}{12}$)=0 | B. | f($\frac{π}{12}$)+f($\frac{3π}{4}$)=0 | C. | f($\frac{π}{12}$)<f($\frac{2π}{3}$) | D. | f(0)>f(-$\frac{5π}{12}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com