
| A. | f(-$\frac{π}{12}$)=0 | B. | f($\frac{π}{12}$)+f($\frac{3π}{4}$)=0 | C. | f($\frac{π}{12}$)<f($\frac{2π}{3}$) | D. | f(0)>f(-$\frac{5π}{12}$) |
分析 由题意可得,当x=$\frac{π}{6}$时,函数f(x)取得最小值,由此求得φ的值,可得函数的解析式,再利用诱导公式、特殊角的三角函数的值,判断各个选项中的不等式是否正确,从而得出结论.
解答 解:∵函数f(x)=sin(2x+φ)满足对一切x∈R,都有f(x)≥f($\frac{π}{6}$)成立,
∴当x=$\frac{π}{6}$时,函数f(x)取得最小值,即2•$\frac{π}{6}$+φ=2kπ-$\frac{π}{2}$,k∈Z,即φ=2kπ-$\frac{5π}{6}$,k∈Z,
故可取φ=-$\frac{5π}{6}$,此时,k=0,为整数,
∴f(x)=sin(2x-$\frac{5π}{6}$).
∴f(-$\frac{π}{12}$)=sin(-π)=-sinπ=0,故A成立;
∵f($\frac{π}{12}$)=sin(-$\frac{2π}{3}$)=-sin$\frac{2π}{3}$=-$\frac{\sqrt{3}}{2}$,f($\frac{3π}{4}$)=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,∴f($\frac{π}{12}$)+f($\frac{3π}{4}$)=0,故B成立;
又 f($\frac{2π}{3}$)=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,∴f($\frac{π}{12}$)<f($\frac{2π}{3}$),故C成立;
f(0)=sin(-$\frac{5π}{6}$)=-sin$\frac{5π}{6}$=-$\frac{1}{2}$,f(-$\frac{5π}{12}$)=sin0=0,故f(0)>f(-$\frac{5π}{12}$)不成立,
故选:D.
点评 本题主要考查正弦函数的最小值,特殊角的三角函数的值,诱导公式,属于基础题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,2e2] | B. | [0,2e3] | C. | (0,2e2] | D. | (0,2e3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | 3或5 | D. | 1或3或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e-1) | B. | (0,e-1) | C. | (e,+∞) | D. | (0,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4} | B. | {1,4} | C. | {3,4} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
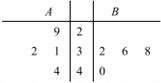 将某商场A,B两个品牌店在某日14:00-18:00四个时段(每个小时作为一个时段)的客流量统计并绘制成如图所示的茎叶图.
将某商场A,B两个品牌店在某日14:00-18:00四个时段(每个小时作为一个时段)的客流量统计并绘制成如图所示的茎叶图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com