
| A. | (-∞,e-1) | B. | (0,e-1) | C. | (e,+∞) | D. | (0,e) |
分析 令lnx=kx得lnx=kx,分别做出y=lnx和y=kx的函数图象,求出y=lnx的过原点的切线的斜率,利用图象得出实数k的范围.
解答 解:令lnx-kx=0得lnx=kx,
做出y=lnx和y=kx的函数图象,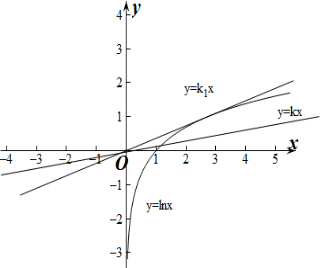
设y=k1x与y=lnx相切,切点为(x0,y0),
∴$\left\{\begin{array}{l}{{y}_{0}={k}_{1}{x}_{0}}\\{{y}_{0}=ln{x}_{0}}\\{\frac{1}{{x}_{0}}={k}_{1}}\end{array}\right.$,解得k1=$\frac{1}{e}$,x0=e,y0=1.
∵方程lnx-kx=0有两个不相等的实数根,
∴y=lnx和y=kx的函数图象有两个交点,
∴0<k$<\frac{1}{e}$.
故选:B.
点评 本题考查了函数的零点个数与函数图象的关系,导数的几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
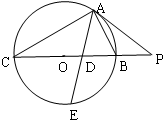 如图,△ABC内接于直径为BC的圆O,过点作圆O的切线交CB的延长线于点P,AE交BC和圆O于点D、E,且$\frac{AC}{AB}$=$\frac{CD}{DB}$,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点作圆O的切线交CB的延长线于点P,AE交BC和圆O于点D、E,且$\frac{AC}{AB}$=$\frac{CD}{DB}$,若PA=2PB=10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 | 晕机 | 不晕机 | 合计 |
| 男 | 24 | 31 | 55 |
| 女 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P-ABC为正三棱锥,底面边长为2,设D为PB的中点,且AD⊥PC,如图所示
已知P-ABC为正三棱锥,底面边长为2,设D为PB的中点,且AD⊥PC,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-$\frac{π}{12}$)=0 | B. | f($\frac{π}{12}$)+f($\frac{3π}{4}$)=0 | C. | f($\frac{π}{12}$)<f($\frac{2π}{3}$) | D. | f(0)>f(-$\frac{5π}{12}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<2 | B. | a<-1或0≤a<2 | C. | -1<a<$\frac{1}{2}$ | D. | a<-1或0≤a<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{13i}{5}$ | B. | -$\frac{13}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com