
| A. | -1<a<2 | B. | a<-1或0≤a<2 | C. | -1<a<$\frac{1}{2}$ | D. | a<-1或0≤a<$\frac{1}{2}$ |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,根据当且仅当x=0,y=2时z=y-ax取得最大值,可得经过定点(0,2)的直线y=ax+z的斜率a∈(-1,2).
解答 解:由约束条件$\left\{\begin{array}{l}x+y-2≤0\\ x-2y-2≤0\\ 2x-y+2≥0\end{array}\right.$作出可行域如图,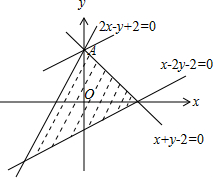
化目标函数z=y-ax为y=ax+z,
∵当且仅当x=0,y=2时z=y-ax取得最大值,
∴经过定点(0,2)的直线y=ax+z的斜率a∈(-1,2).
故选:A.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
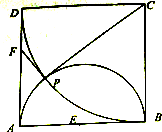 如图,四边形ABCD为正方形,以AB为直径 的半圆E与以C为圆心CB为半径的圆弧相交于点P,过点P作圆C的切线PF交AD于点F,连接CP.
如图,四边形ABCD为正方形,以AB为直径 的半圆E与以C为圆心CB为半径的圆弧相交于点P,过点P作圆C的切线PF交AD于点F,连接CP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e-1) | B. | (0,e-1) | C. | (e,+∞) | D. | (0,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4} | B. | {1,4} | C. | {3,4} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,2] | C. | (-∞,4) | D. | (-∞,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com