
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,x02+1<0”的否定是“?x0∈R,x02+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 若f(x)是R上的偶函数,则f(x+1)的图象的对称轴是x=-1 |
分析 A.根据不等式的关系,结合充分条件和必要条件的定义进行判断即可,
B.根据特称命题的否定是全称命题进行判断,
C.根据充分条件和必要条件的定义结合一元二次方程根的分布进行求解即可,
D.根据偶函数的性质以及函数平移关系进行判断.
解答 解:A.当a=1,b=-1时,满足a>b,但a2>b2不成立,即充分性不成立,故A错误,
B.命题“?x0∈R,x02+1<0”的否定是“?x0∈R,x02+1≥0”,故B错误,
C.若方程x2+(a+1)x+a-2=0的两实根异号,
则$\left\{\begin{array}{l}{△=(a+1)^{2}-4(a-2)>0}\\{{x}_{1}{x}_{2}=a-2<0}\end{array}\right.$,即$\left\{\begin{array}{l}{{a}^{2}-2a+9>0}\\{a<2}\end{array}\right.$,即a<2,
即方程有两实根异号的充要条件是a<2,故C错误,
D.若f(x)是R上的偶函数,则公式f(x)关于y轴即x=0对称,
将函数f(x)向左平移1个单位,得到f(x+1),则函数关于x=-1对称,
即D正确,
故选:D
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,难度不大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
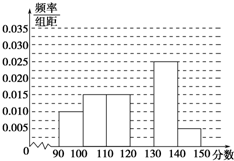 某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:| 数学成绩“优秀” | 数学成绩“一般” | 总计 | |
| 地理成绩“优秀” | 10 | 40 | 50 |
| 地理成绩“一般” | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{3}$,3) | B. | (-∞,-$\frac{1}{3}}$)∪(3,+∞) | C. | (-∞,-3)∪(${\frac{1}{3}$,+∞) | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1,3] | C. | [1,2] | D. | [0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2e2] | B. | [0,2e3] | C. | (0,2e2] | D. | (0,2e3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | 3或5 | D. | 1或3或5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com